Запишем формулу напряжённости электрического поля , где q₀ - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²), е - диэлектрическая проницаемость.
Запишем формулу потенциала точечного заряда , где q - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²).
Выразим напржяённость электрического поля через потенциал точечного заряда:
. В системе СИ 5 нКл = 5*10⁻⁹ Кл. Подставляем числовые занчения и вычисляем искомую величину диэлектрической проницаемости:
№3.
При паралельном соеденении конденсаторов:
Как видим ёмкости складываются. Для данного случая:
Подставим и вычислим искомую величину ёмкости второго заряда:
№4.
По формуле напряжённости электрического поля , где F - действующая сила (Н), q - величина заряда (Кл). Где действующую силу распишим
по формуле второго закона Ньютона , где m - масса тела (кг), а - ускорение тела (м/с²). Масса электрона . Подставим в формулу закона Ньютона: . В системе СИ: 0,8 Тм/с = 0,8*10¹² м/с.
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.
№1. Решение во вложении..!
№2.
Запишем формулу напряжённости электрического поля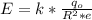 , где q₀ - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²), е - диэлектрическая проницаемость.
, где q₀ - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²), е - диэлектрическая проницаемость.
Запишем формулу потенциала точечного заряда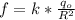 , где q - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²).
, где q - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²).
Выразим напржяённость электрического поля через потенциал точечного заряда:
Выразим искомую величину диэлектрической проницаемости:
№3.
При паралельном соеденении конденсаторов: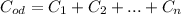
Как видим ёмкости складываются. Для данного случая: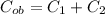
Подставим и вычислим искомую величину ёмкости второго заряда:
№4.
По формуле напряжённости электрического поля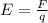 , где F - действующая сила (Н), q - величина заряда (Кл). Где действующую силу распишим
, где F - действующая сила (Н), q - величина заряда (Кл). Где действующую силу распишим
по формуле второго закона Ньютона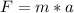 , где m - масса тела (кг), а - ускорение тела (м/с²). Масса электрона
, где m - масса тела (кг), а - ускорение тела (м/с²). Масса электрона 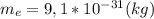 . Подставим в формулу закона Ньютона:
. Подставим в формулу закона Ньютона: 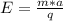 . В системе СИ: 0,8 Тм/с = 0,8*10¹² м/с.
. В системе СИ: 0,8 Тм/с = 0,8*10¹² м/с.
Заряд электрона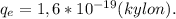 . Подставляем и вычисляем:
. Подставляем и вычисляем:
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.