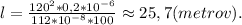В открытых сообщающихся сосудах налитая жидкость всегда устанавливается на одном уровне, например вода внутри чайника и в носике чайника.Действие какого физического закона иллюстрирует этот пример? Сформулируйте этот закон
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомомстержне в однородном поле сил тяготения[1]. Периодмалых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массымаятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
По формуле полезной мощности выделевшейся на внешнем участке цепи , где U - напряжение (В), I - сила тока (А), R - электрическое сопроитивление (Ом). Электричсекое сопростивление расписываем по формуле , где p - удельное сопротивление проводника (Ом*м), l - длина проводника (м), S - поперечное сечение проводника (м²). Подставив данную формулу в формулу мощности получим:
Отсюда выражаем находимую дину проводника: , в системе СИ: 0,2 мм² = 0,2*10⁻⁶ м²; удельное сопроивление нихрома р = 112*10⁻⁸ Ом*м. Подставляем численные данные и вычисляем:
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомомстержне в однородном поле сил тяготения[1]. Периодмалых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит[2] от амплитуды колебаний и массымаятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
По формуле полезной мощности выделевшейся на внешнем участке цепи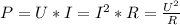 , где U - напряжение (В), I - сила тока (А), R - электрическое сопроитивление (Ом). Электричсекое сопростивление расписываем по формуле
, где U - напряжение (В), I - сила тока (А), R - электрическое сопроитивление (Ом). Электричсекое сопростивление расписываем по формуле 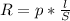 , где p - удельное сопротивление проводника (Ом*м), l - длина проводника (м), S - поперечное сечение проводника (м²). Подставив данную формулу в формулу мощности получим:
, где p - удельное сопротивление проводника (Ом*м), l - длина проводника (м), S - поперечное сечение проводника (м²). Подставив данную формулу в формулу мощности получим: 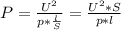
Отсюда выражаем находимую дину проводника: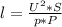 , в системе СИ: 0,2 мм² = 0,2*10⁻⁶ м²; удельное сопроивление нихрома р = 112*10⁻⁸ Ом*м. Подставляем численные данные и вычисляем:
, в системе СИ: 0,2 мм² = 0,2*10⁻⁶ м²; удельное сопроивление нихрома р = 112*10⁻⁸ Ом*м. Подставляем численные данные и вычисляем: