Обозначим импульс первой платформы до столкновения за p1, после столкновения — за p1’,
импульс второй платформы до столкновения — за p2, после столкновения — за p2’.
Импульс вычисляется по формуле p = mv, где m — масса тела, v — его скорость.
Тогда, по закону сохранения импульса:
p1 + p2 = p1’ + p2’
m1v1 + m2v2 = m1v + m2v (v — скорость после столкновения)
m1v1 + m2v2 = v(m1 + m2)
Платформы движутся навстречу друг другу, а значит, скорость (и импульс) одной из них записывается со знаком «плюс», а другой — со знаком «минус». Пусть со знаком «минус» будет скорость второй платформы. Тогда
m1v1 - m2v2 = v(m1 + m2)
Выразим отсюда v:
Подставим значения:
= -0,1 (м/с)
Знак «минус» в ответе говорит о том, что после столкновения платформы двигались в сторону, в которую раньше двигалась вторая платформа (та, чья скорость была взята со знаком «минус»).
Скорость, с которой они двигались в эту сторону равна 0,1 м/с.
ответ: 0,1 м/с
Объяснение:
Обозначим импульс первой платформы до столкновения за p1, после столкновения — за p1’,
импульс второй платформы до столкновения — за p2, после столкновения — за p2’.
Импульс вычисляется по формуле p = mv, где m — масса тела, v — его скорость.
Тогда, по закону сохранения импульса:
p1 + p2 = p1’ + p2’
m1v1 + m2v2 = m1v + m2v (v — скорость после столкновения)
m1v1 + m2v2 = v(m1 + m2)
Платформы движутся навстречу друг другу, а значит, скорость (и импульс) одной из них записывается со знаком «плюс», а другой — со знаком «минус». Пусть со знаком «минус» будет скорость второй платформы. Тогда
m1v1 - m2v2 = v(m1 + m2)
Выразим отсюда v:
Подставим значения:
Знак «минус» в ответе говорит о том, что после столкновения платформы двигались в сторону, в которую раньше двигалась вторая платформа (та, чья скорость была взята со знаком «минус»).
Скорость, с которой они двигались в эту сторону равна 0,1 м/с.
Начальная скорость — 10 м/с.
Ускорение направлено туда же, куда движется тело.
Модуль ускорения — 4 м/с2.
Объяснение:
Координату тела при равноускоренном движении можно рассчитать по формуле
Уравнение из задачи имеет вид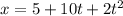 .
.
Если провести аналогию с формулой координаты, получится, что
x0 = 5
10t = v0t, откуда следует, что v0 = 10 (м/с, так как все величины даны в СИ).
Так как ускорение больше 0, оно направлено в ту же сторону, в которую движется тело.