В воде плавает деревянный брусок плотностью 650кг/м³, затем его заменяют на другой брусок плотностью 450 кг/м³. Объем бруска такой же как в первом случае, площадь основания бруска такая же. Как изменился объем погружения второго бруска, глубина погружения, сила тяжести и выталкивающая сила?

Объяснение:

Дано:

x(t) = A·cos (ω·t + φ)

A = 4 см

_______________

φ - ?

Запишем уравнение в виде:

x(t) = 4·cos (ω·t + φ)

Типовое решение данной задачи подробно приведем на примере б). Остальные решаются аналогично!

б)

x(0) = - 2 см;  v(0) < 0

Начальную фазу выразим как:

φ = arcos (x(0)/A) = arccos (-2/4)  = arccos (-1/2)

Значению аргумента (-2) удовлетворяют два значения угла:

φ₁ = π/3   и φ₂ = 2π - π/3 = 5π / 3

Для того, чтобы решить, какое из этих значений угла удовлетворяет условию v(0) < 0 , находим производную:

v(t) = x' = - ω·A·sin (ω·t +φ)

При t=0:

v₁ (0) = - ω·A·sin (π/3) =  - √3 /2· ω·A

v₂ (0) = - ω·A·sin (5·π/3) =  + √3 /2· ω·A

Так как А>0  и ω>0, то условию удовлетворяет только первое значение фазы.

φ = π / 3

Строим диаграмму:

0.8 (г/см^3) * 30 (см^3) * 10 Н/кг = 24 г * 10 Н/кг =

= 0.024 кг *10 Н/кг = 0.24 Н

 - это плотность жидкости.

- это объём тела погружённого в жидкость.

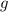 - это ускорение свободного падения = 10 (м/с^2) = 10 Н/кг

1) Нужно найти объём чугунной отливи по формуле: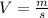  

- масса чугуна,   - плотность чугуна.

V = 20кг/7000(кг/м^3) = 0.003 м^3 (это округлённое значение)

Чтобы удержать чугунную отливку в воде нужно расчитать вес этой чугунной отливки в воде по формуле: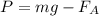  

- вес тела.   - сила тяжести чугуна в воздухе.   - Сила Архимеда

= 20кг * 10 Н/кг = 200Н.

1000(кг/м^3) * 0.003(м^3) * 10 Н/кг = 30Н

Определение букв смотрите в первой задаче.

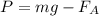= 200Н - 30Н = 170Н

Объяснение: