Здравствуйте. Попробую решить, надеюсь что ход моих рассуждений верен.
Согласно теореме о мгновенном центре скоростей (далее по тексту МЦС), у любого движущегося твердого тела есть такая точка, скорость которой в данный момент времени равна нулю. Движение тела, в данный момент, может быть представлено как поворот тела относительно этой точки. Местоположение этой точки легко найти, достаточно провести перпендикуляры к каким-нибудь двум неколлинеарным векторам скоростей, точка их пересечения и будет МЦС. В нашем случае, уже известно направление скорости , проводим к ней перпендикуляр АО, МЦС лежит где-то на нем. Далее, нам известно, что скорость точки С равна скорости точки А по модулю, здесь стоит вспомнить следующее соотношение из механики твердого тела
где v – скорость данной точки
ω - угловая скорость вращения тела относительно МЦС
R – расстояние от МЦС до данной точки.
С учетом этого, становится ясно, что точка С должна лежать на таком же расстоянии от МЦС, что и точка А, ведь их скорости равны. Исходя из этих соображений, МЦС будет равноудален от точек А и С и совпадет с точкой О, как показано на рисунке. Вся фигура вращается относительно этой точки. Совершенно очевидно, что точка фигуры, лежащая на наименьшем расстоянии от точки О будет обладать и наименьшей скоростью (точка D), а точка лежащая дальше всего – наибольшей (точка В). Дальше просто расчеты.
Обозначим сторону треугольника за а, а угловую скорость вращения относительно МЦC за ω. Найдем длины отрезков OD и OB из геометрических соображений
4
Объяснение:
Здравствуйте. Попробую решить, надеюсь что ход моих рассуждений верен.
Согласно теореме о мгновенном центре скоростей (далее по тексту МЦС), у любого движущегося твердого тела есть такая точка, скорость которой в данный момент времени равна нулю. Движение тела, в данный момент, может быть представлено как поворот тела относительно этой точки. Местоположение этой точки легко найти, достаточно провести перпендикуляры к каким-нибудь двум неколлинеарным векторам скоростей, точка их пересечения и будет МЦС. В нашем случае, уже известно направление скорости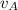 , проводим к ней перпендикуляр АО, МЦС лежит где-то на нем. Далее, нам известно, что скорость точки С равна скорости точки А по модулю, здесь стоит вспомнить следующее соотношение из механики твердого тела
, проводим к ней перпендикуляр АО, МЦС лежит где-то на нем. Далее, нам известно, что скорость точки С равна скорости точки А по модулю, здесь стоит вспомнить следующее соотношение из механики твердого тела
где v – скорость данной точки
ω - угловая скорость вращения тела относительно МЦС
R – расстояние от МЦС до данной точки.
С учетом этого, становится ясно, что точка С должна лежать на таком же расстоянии от МЦС, что и точка А, ведь их скорости равны. Исходя из этих соображений, МЦС будет равноудален от точек А и С и совпадет с точкой О, как показано на рисунке. Вся фигура вращается относительно этой точки. Совершенно очевидно, что точка фигуры, лежащая на наименьшем расстоянии от точки О будет обладать и наименьшей скоростью (точка D), а точка лежащая дальше всего – наибольшей (точка В). Дальше просто расчеты.
Обозначим сторону треугольника за а, а угловую скорость вращения относительно МЦC за ω. Найдем длины отрезков OD и OB из геометрических соображений
Скорость в точке D (минимальная)
Скорость в точке B (максимальная)
Найдем их отношение
я так понимаю, треугольник ABC является абсолютно твёрдым телом?
обозначим единичные векторы направлений сторон e₁, e₂, e₃ (направления AB, BC, AC, соответственно) , а векторы скоростей вершин v₁, v₂, v₃ (вершины A, B, C, соответственно)
в силу нерастяжимости сторон проекции скоростей вершин любой стороны на эту сторону равны, то есть
v₁·e₁=v₂·e₁, v₂·e₂=v₃·e₂, v₃·e₃=v₁·e₃
кроме того из условия следует, что v₂=v e₁ и что v₃=x e₂
векторы e₁, e₂, e₃ единичные, поэтому e₁·e₁=1, e₂·e₂=1, e₃·e₃=1
из геометрии следует, что e₁·e₂=cos 120°=-1/2, e₂·e₃=cos 60°=1/2, e₁·e₃=cos 60°=1/2
подставляя все эти данные в условия нерастяжимости сторон, получим
v₁·e₁=v, -v/2=x, x/2=v₁·e₃
откуда v₁·e₁=v, v₁·e₃=-v/4
пусть v₁=a e₁+b e₃
тогда a+b/2=v, a/2+b=-v/4, откуда a=3v/2, b=-v
v₁²=a²+b²+2ab/2=a²+b²+ab=9v²/4+v²-3v²/2=7v²/4
поэтому |v₁|=(v√7)/2