Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x = = 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Объяснен1. Из условия задачи предполагается, что движение грузовика равноускоренное:
m = 6 т = 6000 кг;
v0 = 36 км/ч = 36 * 1000 м / 3600 c = 10 м/с;
v = 0;
t = 30 c;
v = v0 + at. (1)
2. Из уравнения (1) определим ускорение грузовика:
at = v - v0;
a = (v - v0) / t;
a = (0 - 10) / 30 = -1/3 (с).
3. Вычислим силу торможения:
F = ma = 6000 * (-1/3) = -2000 (Н).
Знак минус означает, что сила торможения направлена против движения грузовика.
ответ: 2000 Н.
вот
ответ: 1.4м/c 1м/c 1м/c 0м/c
Объяснение:
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x =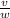
= 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Теперь легко определяем скорости точек C и B:
Vc = ωa = 1м/c
Vb = ω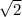
a = 1.4 м/c