Пра́вила Кирхго́фа (часто в технической литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока[1].
Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
Пра́вила Кирхго́фа (часто в технической литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока[1].
Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году[2].
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.
3 и 8 ЗАДАЧУ НЕ РЕШИЛ!
1. Дано: СИ Анализ Решение
m=400г 0,4 кг p=mV p=0,4*4=1,6кг*м/с
V=4м/с
Найти:
p
2. Дано: СИ : Анализ: Решение:
m=2000т 2000000 кг p1=mV1 2000000*10- 2000000*15
V1=54 км/ч 15м/c p2=mV2 20000000-30000000
V2 = 36 км/ч 10м/c mV1-mV2 = -10000000=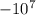
Найти:
p2-p1
4. Дано: СИ Анализ: Решение:
m1=30т 30000кг m1v1 +m2v2 = (m1+m2)u u=30 000 кг ·
V1=1,5 м/c u = (m1v1 +m2v2) / (m1+m2) 1,5/(30000+20
m2=20т 20000кг u =m1v1 / (m1+m2) 000) = 0,9 м/c
V2=0 (т.к. он не подвижен)
Найти:
u
5. Дано: СИ Анализ: Решение:
m1 = 100 кг p1 = m1V1 p1=100*500 = 50 000кг*м/с
V1 = 500 м/с p2 = - m2V2 p2=- 10 000*10=-100 000 кг*м/с
m2 = 10 т 10 000 кг До: Po = P1 + P2 Po= 50 000 - 100 000 = - 50 000
V2 = 36 км/ч 10 м/с После:P = (m1+m2)u mобщ=10010
Найти: P=mобщ*U u= - 50 000/10010=≈ - 4,95
u По закону сохр. импульса:
P = Po,
mобщ*U = Po
u=Po/mобщ
6. Дано: Анализ: Решение:
m1 = 50 кг p = mv v2=50*0.2/(50 + 200)=0.04 м/с
m2 = 200 кг До: p = m1v1 v2-v1=0.2 - 0.04 = 0.16
v1 = 0.2 м/с После: p = (m1 + m2)v
Найти: p = p
V2-V1 m1v1 = (m1 + m2)v
v = m1v1/(m1 + m2)
7. Дано: Анализ: Решение:
m1=120 кг m1v1-m2v2 = (m1+m2)V V=120*6-60*2,5/120+60
v1=6 м/с V=m1v1-m2v2/m1+m2 V=570/180=3,17 м/c
m2=60 кг
v2=2.5 м/с
Найти:
Vчел-?