1. Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен.
2. Когда тела будут иметь равную температуру, теплообмен прекратится.
3. Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус». А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс».
4. Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии. Сохранение тепловой энергии можно записать в виде уравнения теплового баланса. В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене). В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Для початку треба пригадати, що прискорення вільного падіння g = 10 м/с². Звідси можна відразу ж сказати, що хлопчик падав до поверхні води 1 секунду, оскільки висота, з якою він стрибнув, дорівнює 5 метрам. Цю величину можна отримати, якщо використовувати формулу для визначення довжини пройденого шляху при рівноприскореному русі.
S = · t + a · . Але оскільки початкова швидкість хлопчика у вертикальному напрямку дорівнювала 0, то S = a · .
Для випадку падіння, коли прискорення дорівнює g, шлях S = g · . З цього виразу випливає, що t² = .
Підставивши відомі величини, знайдемо, що t² = = 1. Таким чином показано, що час вільного падіння з висоти 5 метрів дорівнює 1 секунді.
Вертикальну швидкість, яку за цей час набере хлопчик, знайдемо за формулою Vв = g · t = 10 · 1 = 10 м/с.
Горизонтальна складова повної швидкості (Vг ) не змінюється і дорівнює 6 м/с.
Вектор повної швидкості в момент торкання хлопчиком води знайдемо по теоремі Піфагора:
Vп² = Vг² + Vв² = 6² + 10² = 136.
Vп ≈ 11,66 м/с.
Кут між вектором швидкості і горизонтом буде дорівнює arctg(Vв/Vг) = arctg() = 59,04°
1. Если тела имеют различную температуру, то между ними возможен обмен тепловой энергией, т. е. теплообмен.
2. Когда тела будут иметь равную температуру, теплообмен прекратится.
3. Тело с высокой температурой, отдает тепловую энергию (теплоту) и остывает. Отданное количество теплоты Q имеет знак «минус». А тело с низкой температурой получает тепловую энергию и нагревается. Полученное количество теплоты Q имеет знак «плюс».
4. Количество теплоты, отданное горячим телом равно количеству теплоты, полученному холодным телом. Это – закон сохранения тепловой энергии. Сохранение тепловой энергии можно записать в виде уравнения теплового баланса. В левой части уравнения складываем количества теплоты (всех тел, участвующих в теплообмене). В правой части уравнения записываем ноль, когда теплообмен с окружающей средой отсутствует.
Для початку треба пригадати, що прискорення вільного падіння g = 10 м/с². Звідси можна відразу ж сказати, що хлопчик падав до поверхні води 1 секунду, оскільки висота, з якою він стрибнув, дорівнює 5 метрам. Цю величину можна отримати, якщо використовувати формулу для визначення довжини пройденого шляху при рівноприскореному русі.
S =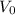 · t + a ·
· t + a · 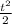 . Але оскільки початкова швидкість хлопчика у вертикальному напрямку дорівнювала 0, то S = a ·
. Але оскільки початкова швидкість хлопчика у вертикальному напрямку дорівнювала 0, то S = a · 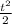 .
.
Для випадку падіння, коли прискорення дорівнює g, шлях S = g ·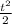 . З цього виразу випливає, що t² =
. З цього виразу випливає, що t² = 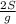 .
.
Підставивши відомі величини, знайдемо, що t² =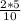 = 1. Таким чином показано, що час вільного падіння з висоти 5 метрів дорівнює 1 секунді.
= 1. Таким чином показано, що час вільного падіння з висоти 5 метрів дорівнює 1 секунді.
Вертикальну швидкість, яку за цей час набере хлопчик, знайдемо за формулою Vв = g · t = 10 · 1 = 10 м/с.
Горизонтальна складова повної швидкості (Vг ) не змінюється і дорівнює 6 м/с.
Вектор повної швидкості в момент торкання хлопчиком води знайдемо по теоремі Піфагора:
Vп² = Vг² + Vв² = 6² + 10² = 136.
Vп ≈ 11,66 м/с.
Кут між вектором швидкості і горизонтом буде дорівнює arctg(Vв/Vг) = arctg(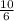 ) = 59,04°
) = 59,04°