Из-за того что ускорение свободного падение на Марсе и на Луне отличаются, периоды одинаковых математических маятников будут разными. Ускорение свободного падения на луне равняется около g= 1,6 м/с². Ускорение свободного падения на Марсе равняется около g=3,7 м/с². Теперь возьмем формулу периода математического маятника T=2π*, и поставим на место g 1,6 и 3,7. После этого возьмем их отношения, то есть поделим их и получаем простую пропорцию = . Тут нам необходимо найти х. х==7,125 раз в минуту.
( 1,9 и 1,26 это 3,7 и 1,6 только уже без квадратного корня )
Выразим V из закона Менделеева-Клапейрона:
P V = m R T / M => V = m R T / P M.
А теперь приравняем V1 к V2. И дабы не писать лишнего, сразу посмотрим, что у нас сократится: M, R, m (но сначала я напишу с m для ясности). Получаем:
m T1 / P1 = 0,4 m T2 / P2.
У тебя сейчас, наверное, возник вопрос: почему во второй части уравнения перед m стоит 0,4?
- Потому что исходя из условия задачи мы можем сделать вывод, что m2 = 0,4 m1 (в уравнении m1 заменена на просто m для краткости).
Теперь сокращаем массы, выводим P2:
P2 = 0,4 T2 P1 / T1 = 4*10^-1 * 273 * 2*10^5 / 3*10^2 = 72,8*10^3 Па
7,125 раз.
Объяснение:
Из-за того что ускорение свободного падение на Марсе и на Луне отличаются, периоды одинаковых математических маятников будут разными. Ускорение свободного падения на луне равняется около g= 1,6 м/с². Ускорение свободного падения на Марсе равняется около g=3,7 м/с². Теперь возьмем формулу периода математического маятника T=2π*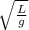
, и поставим на место g 1,6 и 3,7. После этого возьмем их отношения, то есть поделим их и получаем простую пропорцию 
= 
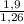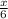. Тут нам необходимо найти х. х=
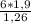=7,125 раз в минуту.
( 1,9 и 1,26 это 3,7 и 1,6 только уже без квадратного корня )