У нас два момента силы М1 и М2 (слева и справа от центра рычага)
M1 = F1 · L1
M2= F2 · L2
Ну и приравниваем их так как моменты всё же РАВНЫ M1=M2
F1 · L1 = F2 · L2
Если моменты силы равны тот рычаг будет в РАВНОВЕСИИ. Это нам надо и выяснить.
Предположим что каждая гиря - 1Дж, каждое деление на рычагу 1 см.
Подсчитываем что там на рисунке и подставляем в формулу
На первом рисунке (слева)
слева рычага: L1 = 4 см ; F1 = 1 Дж
M1 = F1 · L1
М1 = 4 * 1 ; М1 = 4
справа рычага: L = 2 см ; F = 2 Дж
M2 = F2 · L2
М2 = 2 *2 ; М2 = 4
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
На втором рисунке (справа)
слева рычага: L1 = 2 см ; F1 = 3 Дж
M1 = F1 · L1
М1 = 2 * 3 ; М1 = 6
справа рычага: L = 3 см ; F = 2 Дж
M2 = F2 · L2
М2 = 3 *2 ; М2 = 6
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
Давай немного теории:
Сила, с которой тело давит на опору , называют весом.
Вес тела обозначают P и измеряют в ньютонах ( H ) ( а если в килограммах то в 9,8 раз меньше m=, это будет уже масса). Если у тебя 45 кг - это твоя масса, а весишь ты 450 Ньютон. То есть давишь на весы с силой 450 Ньютон.
Любую силу обозначают через F . Хотя в данном случае можно применить Р.
Произведение модуля силы, вращающей тело, на её плечо называется моментом силы.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов, можно записать в виде формулы: M1=M2 .
Это очень элементарно. T - это сила натяжения нити, она действует вертикально, как на верхний шар, так и на нижний, но только в противоположные стороны. Верхний шар нить тянет вниз, а нижний вверх. Обозначим силу тяжести верхнего шара mg, тогда T = 0,5mg. Так же мы можем mg записать, как Vρg, где ρ – плотность материала, из которого изготовлен шар, а V – объём шар. На нижний шар так же действует Архимедова сила Fа, равная его разности его веса и силы натяжения нити. m(второго шара)g = Vρ(второго шара)g. Т.к. объёмы шаров одинаковые, то по сути нам надо найти отношение их плотностей… Как я говорил уже ранее сила Архимеда равна разности веса второго шара и силе натяжения нити - Vρ(второго шара)g - 0,5Vρg = Vρ (воды)g. Сократим одинаковые множители и получим - ρ(второго шара) - 0,5ρ =ρ(воды). Теперь найдём плотность, из которого изготовлен верхний шар – Vρ + 0,5Vρ=0,75ρ(воды) => 1,5Vρ=0,75ρ(воды) => 2Vρ=1ρ(воды). Вернёмся к первому равенству ρ(второго шара) - 0,5ρ =ρ(воды) и внесём изменения – ρ(второго шара) - 0,5ρ =2ρ, т.к. нам известно, что 2ρ=1ρ(воды), перенесём вычитаемое за знак равно и получим что ρ(второго шара)=2,5ρ. Мы получили ответ 2,5ρ. Так же мы можем узнать больше, чем отношение их плотностей, мы можем узнать сами их плотности. Плотность верхнего шара ρ = 500 кг/м^3, ρ(второго шара) = 1250 кг/м^3.
На обеих рисунках рычаги в равновесии
Объяснение:
У нас два момента силы М1 и М2 (слева и справа от центра рычага)
M1 = F1 · L1
M2= F2 · L2
Ну и приравниваем их так как моменты всё же РАВНЫ M1=M2
F1 · L1 = F2 · L2
Если моменты силы равны тот рычаг будет в РАВНОВЕСИИ. Это нам надо и выяснить.
Предположим что каждая гиря - 1Дж, каждое деление на рычагу 1 см.
Подсчитываем что там на рисунке и подставляем в формулу
На первом рисунке (слева)
слева рычага: L1 = 4 см ; F1 = 1 Дж
M1 = F1 · L1
М1 = 4 * 1 ; М1 = 4
справа рычага: L = 2 см ; F = 2 Дж
M2 = F2 · L2
М2 = 2 *2 ; М2 = 4
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
На втором рисунке (справа)
слева рычага: L1 = 2 см ; F1 = 3 Дж
M1 = F1 · L1
М1 = 2 * 3 ; М1 = 6
справа рычага: L = 3 см ; F = 2 Дж
M2 = F2 · L2
М2 = 3 *2 ; М2 = 6
Моменты ОДИНАКОВЫ, значит РАВНОВЕСИЕ
Давай немного теории:
Сила, с которой тело давит на опору , называют весом.
Вес тела обозначают P и измеряют в ньютонах ( H ) ( а если в килограммах то в 9,8 раз меньше m=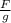
, это будет уже масса). Если у тебя 45 кг - это твоя масса, а весишь ты 450 Ньютон. То есть давишь на весы с силой 450 Ньютон.
Любую силу обозначают через F . Хотя в данном случае можно применить Р.
Произведение модуля силы, вращающей тело, на её плечо называется моментом силы.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов, можно записать в виде формулы: M1=M2 .
Момент силы M = F · L
В 2.5 раза.
Объяснение:
Это очень элементарно. T - это сила натяжения нити, она действует вертикально, как на верхний шар, так и на нижний, но только в противоположные стороны. Верхний шар нить тянет вниз, а нижний вверх. Обозначим силу тяжести верхнего шара mg, тогда T = 0,5mg. Так же мы можем mg записать, как Vρg, где ρ – плотность материала, из которого изготовлен шар, а V – объём шар. На нижний шар так же действует Архимедова сила Fа, равная его разности его веса и силы натяжения нити. m(второго шара)g = Vρ(второго шара)g. Т.к. объёмы шаров одинаковые, то по сути нам надо найти отношение их плотностей… Как я говорил уже ранее сила Архимеда равна разности веса второго шара и силе натяжения нити - Vρ(второго шара)g - 0,5Vρg = Vρ (воды)g. Сократим одинаковые множители и получим - ρ(второго шара) - 0,5ρ =ρ(воды). Теперь найдём плотность, из которого изготовлен верхний шар – Vρ + 0,5Vρ=0,75ρ(воды) => 1,5Vρ=0,75ρ(воды) => 2Vρ=1ρ(воды). Вернёмся к первому равенству ρ(второго шара) - 0,5ρ =ρ(воды) и внесём изменения – ρ(второго шара) - 0,5ρ =2ρ, т.к. нам известно, что 2ρ=1ρ(воды), перенесём вычитаемое за знак равно и получим что ρ(второго шара)=2,5ρ. Мы получили ответ 2,5ρ. Так же мы можем узнать больше, чем отношение их плотностей, мы можем узнать сами их плотности. Плотность верхнего шара ρ = 500 кг/м^3, ρ(второго шара) = 1250 кг/м^3.