Пусть v - искомая скорость пули, m - её масса. Кинетическая энергия пули E=m*v²/2 Дж. По условию, при ударе пули о перегородку выделяется количество теплоты Q=0,488*E=0,244*m*v² Дж. Для того, чтобы расплавить пулю, её надо сначала нагреть до температуры плавления. Для этого требуется количество теплоты Q1=120*m*(603-303)=36000*m Дж. Затем пуля начинает плавиться, на её расплавление необходимо количество теплоты Q2=25000*m Дж. Таким образом, для расплавления пуля должна иметь минимальную скорость, определяемую условием Q=Q1+Q2. Отсюда следует уравнение 0,244*m*v²=36000*m+25000*m, или 0,244*v²=61000. Отсюда v²=61000/0,244=250000 м²/с² и v=√250000=500 м/с. ответ: при скорости 500 м/с.
Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника: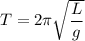 .
.
2. Выразим длину: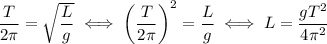 .
.
3. Численно получим: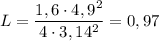 (м).
(м).
ответ: 0,97 м.======================Задача #2Дано: C =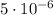 Ф; T = 0,001 c. Найти: L - ?
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона: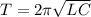 .
.
2. Индуктивность из (1):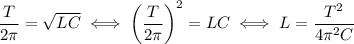 .
.
3. Численно получим: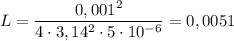 (Гн).
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
ответ: 5,1 мГн.======================Задача #3Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде: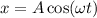 , отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты: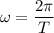 , значит период:
, значит период: 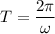 .
.
3. Численно: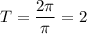 (c).
(c).
ответ: 0,4 м; 2 с.График зависимости x(t) смотри в приложении.