Во сколько раз мощность двигателя электровоза фирмы тальго превышает мощность двигателя самосвала производства казахстанско-российского предприятия ао камаз-инжиниринг в городе кокшетау? мощность двигателя электровоза достигает 7200к, вт мощность двигателя самосвала 190 квт. сравните силу тяги
двигателей, если скорость поезда равна 140км/ч,а скорость самосвала 80 км/ч. , это д/з и я не тороплюсь, есть много других учеников которым нужна , им всё таки нужнее
В момент времени t = 1 с ускорения точек были одинаковы, относительная скорость точек v₂₋₁ = 3 м/с, точки находились на расстоянии 5 м друг от друга
Объяснение:
При движении координата 1-й точки изменяется по закону
x₁(t) = 1 + 7t + t² + 2t³
Скорость движения 1-й точки
v₁(t) = x' = 7 + 2t + 6t²
Ускорение движения 1-й точки
a₁(t) = v₁'(t) = 2 + 12t
Ускорение движения 2-й точки задано
a₂(t) = 8 + 6t
Момент времени t, в который ускорения точек одинаковы, определим из уравнения
2 + 12t = 8 + 6t
6t = 6
t = 1 (с)
Cкорость движения 2-й точки
v₂(t) =v₂₀ + ∫a₂(t) dt = 1 + ∫(8 + 6t) dt = 1 + 8t +3t²
В моvент времени t = 1 скорости точек
v₂(1) = 1 + 8 + 3 = 12 (м/с)
v₁(t) = 7 + 2 + 6 = 15 (м/с)
Относительная скорость
v₂₋₁ = v₁(t) - v₂(1) = 15 - 12 = 3 (м/с)
Координата 2-й точки
х₂(е) = х₂₀ + ∫v₂(t) d = ∫(1 + 8t + 3t²) dt = t + 4t² + t³
В моvент времени t = 1 координаты точек
x₁(1) = 1 + 7 + 1 + 2 = 11 (м)
х₂(1) = 1 + 4 + 1 = 6 (м)
Точки находились друг от друга на расстоянии
s₁₋₂ = 11 - 6 = 5 (м)
Закон Гаусса:
Поток напряженности электрического поля через произвольную поверхность, окружающую тело, равен заряду тела, умноженному на 4π.
Окружим заряженный шар сферой, радиуса r.
Сначала положим r>R, где R - радиус шара.
Из вышеописанного закона:
Из симметричности задачи следует, что напряженность E в каждой точке сферы r одинакова (и направлена вдоль радиуса), то есть E=const в подинтегральм выражении. Тогда:
Отсюда: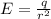 .
.
Для нахождения поля внутри шара, при r<R, введем объемную плотность заряда:
Аналогично, найдем поток напряженности поля через сферу, радиуса r. Точно также, из симметрии, считаем E = const (на этой сфере). Тогда:
Здесь, q_{in} - заряд шара, радиуса r:
Подставляя в выражение для E, получим:
Ниже представлен график модули напряженности электрического поля для всех r.