Во время лабораторной работы ученик проверял условие равновесия рычага. Какой массы груз, отмеченный на рисунке знаком "?", должен выбрать ученик, чтобы рычаг оказался в состоянии равновесия? ответ дайте в г. Ускорение свободного падения принять равным 10
. —
. c²
решение
t= t1+t2 t1=L/(V1-V2) V2=9 км/ч=2,5 м/с
t2=L/(V1+V2)
120=36/(V1-2,5)+36/(V1+2,5) V1=X
после преобразований получаем
10*x^2-6*x -62,5=0
x=2,8 2м/с
2) Автомобиль за проходит первую треть пути с некоторой постоянной скоростью, а оставшуюся часть пути со скоростью 72км/ч. Определите скорость движения автомобиля на первом участке, если его средняя скорость на всем пути равна 54км/ч.
Vср=S/t=S/(t1+t2)=S/(S/3*V1 +2*S/3*V2)=3/(1/V1+2/V2)
Vcр=3*V1*V2/(V2+2*V1)
54=3*X*72/(72+2*X)
X=36 км/ч=10 м/с
3) В отсутствие ветра парашютист опускается на землю со скоростью 4м/с. С какой скоростью он будет двигаться при горизонтальном ветре, скорость ветра равна 3м/с
скорости складываются как вектора
V=√V1²+V2²=√25=5 м/с - ответ
<U> = 61.7 км/ч
Объяснение:
через время:
мы знаем что у нас два одинаковых участка пути.
Значит S₁ = S₂ =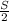
Мы знаем скорость и время прохождения второй половины пути.
Найдём расстояние.
S₂ = U₂t₂ = 54 км/ч * 4 ч. = 216 км - вторая половина пути.
S₁ = S₂ = 216 км.
Найдём время прохождения первого участка.
t₁ =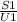 = 3 часа.
= 3 часа.
<U> =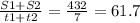 км/ч
км/ч
т.к. у нас одинаковые отрезки путей, можем использовать формулу:
<U> =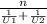 , где n - кол-во отрезков путей. У нас их 2. Подставим и посчитаем, получится 61.7 км/ч.
, где n - кол-во отрезков путей. У нас их 2. Подставим и посчитаем, получится 61.7 км/ч.