Поток напряженности электрического поля через произвольную поверхность, окружающую тело, равен заряду тела, умноженному на 4π.
Окружим заряженный шар сферой, радиуса r.
Сначала положим r>R, где R - радиус шара.
Из вышеописанного закона:
, где интеграл берется по поверхности радиуса r.
Из симметричности задачи следует, что напряженность E в каждой точке сферы r одинакова (и направлена вдоль радиуса), то есть E=const в подинтегральм выражении. Тогда:
.
Отсюда: .
Для нахождения поля внутри шара, при r<R, введем объемную плотность заряда:
.
Аналогично, найдем поток напряженности поля через сферу, радиуса r. Точно также, из симметрии, считаем E = const (на этой сфере). Тогда:
.
Здесь, q_{in} - заряд шара, радиуса r:
.
Подставляя в выражение для E, получим:
.
Ниже представлен график модули напряженности электрического поля для всех r.
Закон Гаусса:
Поток напряженности электрического поля через произвольную поверхность, окружающую тело, равен заряду тела, умноженному на 4π.
Окружим заряженный шар сферой, радиуса r.
Сначала положим r>R, где R - радиус шара.
Из вышеописанного закона:
Из симметричности задачи следует, что напряженность E в каждой точке сферы r одинакова (и направлена вдоль радиуса), то есть E=const в подинтегральм выражении. Тогда:
Отсюда: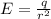 .
.
Для нахождения поля внутри шара, при r<R, введем объемную плотность заряда:
Аналогично, найдем поток напряженности поля через сферу, радиуса r. Точно также, из симметрии, считаем E = const (на этой сфере). Тогда:
Здесь, q_{in} - заряд шара, радиуса r:
Подставляя в выражение для E, получим:
Ниже представлен график модули напряженности электрического поля для всех r.
Відповідь:
10 г
Пояснення:
Коли зігнули дріт, центр мас лівої частинки перемістився на відстань L/4 ближче до точки підвішування, де L- довжина половини.
Тоді початковий момент сил був M=mgL/4 (бо відстань до т. підвішування була L/2 і маса лівої частини була m/2 )
Тепер момент сил можна знайти за формулою M1=mgL/8
Тоді додатковий момент сил, який створює вантаж- M2=m1gL/2
Тоді M1+M2=M
Підставимо попередні формули в останню m1gL/2+mgL/8=mgL/4
m1=m/4=40 г/4=10 г
Когда согнули проволока, центр масс левой частицы переместился на расстояние L / 4 ближе к точке подвешивания, где L- длина половины.
Тогда начальный момент сил был M = mgL / 4 (ибо расстояние до т. Подвешивания была L / 2 и масса левой части была m / 2)
Теперь момент сил можно найти по формуле M1 = mgL / 8
Тогда дополнительный момент сил, который создает вантаж-
M2 = m1gL / 2
Тогда M1 + M2 = M
Подставим предыдущие формулы в последнюю m1gL / 2 + mgL / 8 = mgL / 4
m1 = m / 4 = 40 г / 4 = 10 г