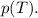Воздушный конденсатор емкостью 6 нф, подключенный к батарее напряжением 12 в, заполняют парафином. какой заряд (нкл) пройдет при этом по цепи? парафин=2.2
Частоту электромагнитных волн, которые принимает радиоприемник, можно определить по формуле:
ν=12πLC−−−√(1)
В этой формуле L – индуктивность катушки радиоприемника, C – общая электроемкость конденсаторов радиоприемника.
Известно, что электромагнитные волны распространяются со скоростью света c (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света c), частотой их колебаний ν и длиной волны λ существует следующее соотношение:
c=λν
λ равна:
λ=cν
В эту формулу подставим выражение (1):
λ=2πcLC−−−√(2)
Известно, что параллельно соединенные конденсатора емкостью C1 и C2 имеют общую емкость C, которую можно определить по формуле:
Решение. Применим закон Авогадро: в равных объемах газов при одинаковых температурах и давления содержится одинаковое количество молекул:
где Дж/К — постоянная Больцмана.
Поскольку объем газа не изменяется, то есть имеем изохорный процесс:
Определим количество молекул в начале:
Определим количество молекул в конце:
Тогда число молекул газа изменилось на:
Определим значение искомой величины:
ответ: число молекул увеличилось на
2. Дано:
см² м²
Па
Найти:
Решение. Поскольку бутылку закрыли плотно, то объем газа не изменяется. Значит, имеем изохорный процесс. Изохорный процесс описывается законом Шарля: для данной массы газа отношение давления газа к его температуре является постоянным, если объем газа не меняется:
Сила давления — сила, действующая перпендикулярно к поверхности:
Поскольку сила трения — это внешняя сила, то ее значение равно произведению изменения давления на площадь поперечного сечения пробки:
, откуда
Значит,
Определим значение искомой величины:
ответ: 400 К.
3. Имеем циклический процесс макроскопических параметров. Здесь:
Объяснение:
Дано:
L=10 мГн, C1=360 пФ, C2=40 пФ, λ−?
Решение задачи:
Частоту электромагнитных волн, которые принимает радиоприемник, можно определить по формуле:
ν=12πLC−−−√(1)
В этой формуле L – индуктивность катушки радиоприемника, C – общая электроемкость конденсаторов радиоприемника.
Известно, что электромагнитные волны распространяются со скоростью света c (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света c), частотой их колебаний ν и длиной волны λ существует следующее соотношение:
c=λν
λ равна:
λ=cν
В эту формулу подставим выражение (1):
λ=2πcLC−−−√(2)
Известно, что параллельно соединенные конденсатора емкостью C1 и C2 имеют общую емкость C, которую можно определить по формуле:
C=C1+C2
Подставив это выражение в формулу (2), получим:
λ=2πcL(C1+C2)−−−−−−−−−−√
Численный ответ задачи равен:
λ=2⋅3,14⋅3⋅10810⋅10–3⋅(360⋅10–12+40⋅10–12)−−−−−−−−−−−−−−−−−−−−−−−−−−√=3768м
ответ: 3768 м.
Источник: https://easyfizika.ru/zadachi/kolebaniya-i-volny/elektricheskij-kolebatelnyj-kontur-radiopriemnika-soderzhit-katushku-induktivnosti
1. Дано:
Найти: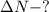
Решение. Применим закон Авогадро: в равных объемах газов при одинаковых температурах и давления содержится одинаковое количество молекул:
где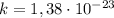 Дж/К — постоянная Больцмана.
Дж/К — постоянная Больцмана.
Поскольку объем газа не изменяется, то есть имеем изохорный процесс: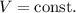
Определим количество молекул в начале:
Определим количество молекул в конце:
Тогда число молекул газа изменилось на:
Определим значение искомой величины:
ответ: число молекул увеличилось на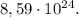
2. Дано:
Найти: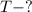
Решение. Поскольку бутылку закрыли плотно, то объем газа не изменяется. Значит, имеем изохорный процесс. Изохорный процесс описывается законом Шарля: для данной массы газа отношение давления газа к его температуре является постоянным, если объем газа не меняется:
Сила давления — сила, действующая перпендикулярно к поверхности:
Поскольку сила трения — это внешняя сила, то ее значение равно произведению изменения давления на площадь поперечного сечения пробки:
Значит,
Определим значение искомой величины:
ответ: 400 К.
3. Имеем циклический процесс макроскопических параметров. Здесь:
Изобразим этот процесс в координатах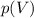 и
и