Вычисли период собственных колебаний колебательного контура, если индуктивность катушки L= 18 мкГн, а ёмкость конденсатора C= 950 пФ. (ответ округли до сотых.)
ОЧЕНЬ

11,25 м

Объяснение:

Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:

Откуда:

Горизонтальная составляющая скорости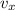 будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):

м/с

Искомый радиус кривизны траектории:

м.

Объяснение:

№1

P = IU = I²R

P1/P2 = ( ( 2I )²( R/4 ) )/( I²R ) = ( I²R )/( I²R ) = 1

№2

η = Рпол./Рзат. * 100%

η = ( I2U2 )/( I1U1 ) 100%

I1 = ( I2U2 )/( ηU1 ) 100%

I1 = ( 9 * 22 )/( 90% * 220 ) 100% = 1 A

№3

λ = Тv

λ = 2π√( LCоб. )v

λ = 2π√( L( C1 + C2 ) )v

λ = 2 * 3,14 √( 10 * 10^-3 ( 360 * 10^-12 + 40 * 10^-12 ) ) 3 * 10^8 = 2 * 3,14 √( 10^-2 ( ( 36 + 4 ) 10^-11 ) 3 * 10^8 = 3768 м

№4

WC( max ) = ( CU( max )² )/2

WL( max ) = ( LI( max )² )/2

W = WC( max ) = WL( max )

( CU( max )² )/2 = ( LI( max )² )/2

CU( max )² = LI( max )²

С = ( LI( max )² )/( U( max )² )

W = WC + WL

W = ( CU² )/2 + ( LI² )/2

( CU( max )² )/2 = ( CU² )/2 + ( LI² )/2

CU( max )² = CU² + LI²

LI( max )² = ( LI( max )²U² )/U( max )² + LI²

LI( max )² = L ( I( max )²U² )/U( max )² + I² )

I( max )² = ( I( max )²U² )/U( max )² + I²

Подставим численные данные и решим уравнение

( 5 * 10^-3 )² = ( ( 5 * 10^-3 )²U²/2² ) + ( 3 * 10^-3 )²

2,5 * 10^-5 = 6,25 * 10^-6U² + 9 * 10^-6

( 25 - 9 ) 10^-6 = 6,25 * 10^-6U²

16 = 6,25U²

U = √( 16/6,25 ) = 1,6 B