Вычислите абсолютную погрешность Δt прямого измерения температуры (для t1=24С°)
Δt = Δи t + Δо t.

Показать ответ

Ответ:

spashkova6

18.09.2022 08:05

1.сколько всего созвездий на небе?

2.сколько звезд можно насчитать невооруженным глазом на небе?

3.запишите название любого созвездия.

4.какой буквой обозначается самая яркая звезда?

5.в состав какого созвездия входит полярная звезда?

6.какие виды телескопов вы знаете?

7.назначение телескопа.

8.назовите известные вам типы небесных тел.

9.назовите любую, известную вам звезду.

10.специальные научно – исследовательское учреждение для наблюдений.

11.чем характеризуется звезда на небе в зависимости от видимой яркости.

12.светлая полоса, пересекающая небо и видимая в яркую звездную ночь.

ответы:

1. 88

2. около 6000

3. что угодно ; )

4. α-альфа

5. м. медведица

6. рефлектор, рефрактор, зеркально-линзовый

7. увеличивает угол зрения, собирает большие света

8. планеты, спутники, кометы и т.д

9. что угодно

10. обсерватория

11. звездные величины

12. млечный путь

0,0(0 оценок)

Ответ:

Ruslan0320

12.05.2023 07:30

Смотреть ниже.

Объяснение:

В своей экспериментальной установке воспользуемся телом некоторой массы и наклонной плоскостью соответственно. Будем перемещать с силы F это тело с самого начала наклонной плоскости и до самого её конца, то есть до некоторой высоты h. Так же допустим, что у этой плоскости негладкая поверхность и коэффициент трения которой равен μ. То есть, на тело будет действовать сила трения Fтр.

Воспользуемся формулой для вычисления КПД наклонной плоскости.

КПД вычисляется по формуле:

$n = \frac{An}{A_{3}} * 100$

Полезной работой будет являться сообщению телу потенциальной энергии, то есть:

$E_{n} = mgh$

где h - высота, м

g - ускорение свободного падения, 9.81 м / с ²

m - масса тела, кг

Затраченной работой будут работы совершённые силой F и Fтр, то есть:

$A = FS + F_{TP}S$ ( угол между линией перемещения и векторами сил равен нулю )

где F - сила, с которой тело перемещается на высоту h, H

Fтр - сила трения, действующая на тело, H

S - длина наклонной плоскости, м

Итого КПД получается равным:

$n = \frac{mgh}{FS + F_{TP}} * 100$

Теперь рассмотрим саму наклонную плоскость. Конкретно нас интересует, как будет изменяться высота подъёма при изменении угла наклона плоскости. Длина наклонной плоскости остаётся постоянной ( S = const и следовательно Aз = const) .

Наклонная плоскость представляет собой прямоугольный треугольник, где d и h катеты треугольника и S гипотенуза треугольника ( ниже представлена схема) . Чтобы найти высоту наклонной плоскости, нужно длину наклонной плоскости умножить на синус угла α. То есть:

$1) sin\alpha = \frac{h}{S}$

$2) h = sin\alpha S$

Допустим, что угол наклона нашей плоскости составляет 45°. Если мы будем увеличивать угол наклона, то получим, что значения градусной меры угла α будут увеличиваться и будут приближаться к значению 90°, где синус максимален и равен 1 ( sinα = 1 ) . Это можно проследить на тригонометрической окружности. Соответственно, исходя из равенства ( 2 ) заметим, что при увеличении угла до значений значений 45 < α < 90° увеличивается синус угла, и получается, что высота, на которую перемещается предмет, увеличивается. И наоборот, если будем брать значения угла 0 < α < 45, то высота, на которую будет перемещаться предмет будет уменьшаться. А это значит, что при изменении высоты, изменяется потенциальная энергия тела: при увеличении высоты h потенциальная энергия возрастает и соответственно КПД наклонной плоскости возрастает, а при уменьшении высоты h потенциальная энергия уменьшается и соответственно КПД наклонной плоскости уменьшается ( помним, что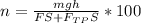 $n = \frac{mgh}{FS + F_{TP}S} * 100$ ) .