Які умови мають виконуватись для того щоб тіло плавало в товщі рідини?

Дано:
= 37 кПа
=
V=13л=0,013
РО(плотность гелия) = 0,179 кг/

Решение:
При изохорном процессе - V и m - const.
Поэтому применим закон Шарля:  =  \frac{p _{2} }{ T_{2} } 

1) =  \frac{p _{2} }{ T_{2} } ⇒ 4**=* ⇒ =148000Па

2) Найдем массу 13л гелия:

m=плотность*объем=0,179*0,013=0,002327кг

3) Из уравнения состояния идеального газа найдем термодинамическую температуру гелия при давлении 148000Па и объеме 13л:

T= ⇒ T=398К=С

4) По условиям задачи Гелий нагревали и его температура возросла в 4 раза, а значит первоначальная температура была 125/4=

5) Формула для нахождения количества теплоты: Q=cm(), где с-удельная теплоемкость гелия при постоянном давлении = 

Q=496500 Дж

ответ: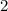 °С

Объяснение:

Дано:

°С

°С

------------------

Пусть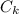 - теплоемкость калориметра

- теплоемкость воды в ложке

- начальная температура калориметра

- конечная температура калориметра

- температура воды в ложке

Теперь запишем уравнение теплового баланса после того как мы влили первую ложку воды в пустой калориметр

- уравнение (1)

Аналогично и для второго случая

- уравнение (2)

В уравнении (2) фигурирует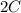 так как это уже "вторая ложка"

Получаем систему из уравнений (1) и (2)

Разделим уравнение уравнение (1) на (2)

Подставляя численные значения упростим

°С

Тогда подставляя это в уравнение в уравнение (1) получим

После вливания в калориметр третьей ложки получим что

                     

Если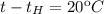   то

°С

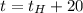
Допустим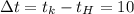   °С

Тогда

°С