В модели Резерфорда угол рассеяния зависит при прочих постоянных от прицельного параметра (т.е. от расстояния между ядром и первоначальным направлением полета частицы). Зависимость следующая
Проще говоря, если частица врежется прямо в ядро ( b = 0 ), из этой формулы следует что угол рассеяния , т.е. он большой, частица полетит назад.
Ну так вот, как много частиц из потока имеют необходимую величину прицельного параметра? Чтоб можно было полететь назад?
ответ дает формула Резерфорда, утверждающая что
(#)
Поясню обозначения
- число частиц, испытывающих рассеяние в углах от
- общее число частиц в потоке, что летит на металлическую фольгу
А теперь посмотрите на график (#) в прикр. файлах
Видно что относительное число частиц, рассеянных на углах близких к 180 градусам, очень мало. В то же время на небольших углах это число велико. Поэтому в силу этой модели можем утверждать, что лишь малая часть отклониться на большие углы.
Если начертить окружность , выбрать точку и из неё провести две линии - одна - радиус к центру, и другая - отрезок равный радиусу как хорду. Достроим треугольник, соединяя центр с точкой пересечения хорды с окружностью. Получим равносторонний треугольник - все стороны равны R.
углы в равностороннем треугольнике по 60°. Получается, что 1 оборот - 360° точка проходит за период, тогда 60° - за шестую часть периода.
t=T/6
За 1/6 долю периода обращения модуль перемещения точки будет равен радиусу окружности.
В модели Резерфорда угол рассеяния зависит при прочих постоянных от прицельного параметра (т.е. от расстояния между ядром и первоначальным направлением полета частицы). Зависимость следующая
Проще говоря, если частица врежется прямо в ядро ( b = 0 ), из этой формулы следует что угол рассеяния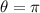 , т.е. он большой, частица полетит назад.
, т.е. он большой, частица полетит назад.
Ну так вот, как много частиц из потока имеют необходимую величину прицельного параметра? Чтоб можно было полететь назад?
ответ дает формула Резерфорда, утверждающая что
Поясню обозначения
А теперь посмотрите на график (#) в прикр. файлах
Видно что относительное число частиц, рассеянных на углах близких к 180 градусам, очень мало. В то же время на небольших углах это число велико. Поэтому в силу этой модели можем утверждать, что лишь малая часть отклониться на большие углы.
Если начертить окружность , выбрать точку и из неё провести две линии - одна - радиус к центру, и другая - отрезок равный радиусу как хорду. Достроим треугольник, соединяя центр с точкой пересечения хорды с окружностью. Получим равносторонний треугольник - все стороны равны R.
углы в равностороннем треугольнике по 60°. Получается, что 1 оборот - 360° точка проходит за период, тогда 60° - за шестую часть периода.
t=T/6
За 1/6 долю периода обращения модуль перемещения точки будет равен радиусу окружности.