Кратчайший путь - это путь, перпендикулярный берегам реки. В таком случае лодка должна противодействовать течению реки, чтобы её не сносило в сторону, когда она поплывёт перпендикулярно берегам. Ведь если она не будет противодействовать, то путь окажется не перпендикулярным, а диагональным. Получается, что cкорость лодки должна быть направлена под тупым углом (π/2 + α) к направлению скорости течения и, следовательно, к берегу, от которого лодка движется, т.к. течение реки происходит параллельно этому берегу. Сделаем расклад скорости лодки на вертикальную составляющую и горизонтальную составляющую. У нас получится прямоугольный треугольник, в котором гипотенуза - это скорость лодки относительно воды v, катет, параллельный берегу, - скорость течения v', и катет, перпендикулярный берегу, - скорость лодки относительно берега V. Угол β - острый угол между скоростью v и берегом, который нам и нужно будет найти. Выходит, что скорость относительно берега равна геометрической разности скорости относительно воды и скорости течения:
Найдём угол β между направлением скорости лодки v и берегом из соотношения катетов прямоугольного треугольника - поделим скорость V (противолежащий катет) на скорость v' (прилежащий катет):
Остаётся найти перемещение лодки относительно воды. Т.к. горизонтальная составляющая скорости лодки относительно воды v по модулю равна скорости течения v', то абсолютная скорость лодки в системе отсчёта "вода" равна этой же скорости:
Vabs = |v'| = v' = 3 м/с
За время t лодка переместится относительно воды по горизонтали на расстояние:
D = Vabs*t = 3*50 = 150 м
По вертикали лодка переместится на расстояние L, тогда полное перемещение лодки s будет равно геометрической сумме L и D:
Дано:
L = 200 м
v = 5 м/с
v' = 3 м/с
V, t, β, s - ?
Кратчайший путь - это путь, перпендикулярный берегам реки. В таком случае лодка должна противодействовать течению реки, чтобы её не сносило в сторону, когда она поплывёт перпендикулярно берегам. Ведь если она не будет противодействовать, то путь окажется не перпендикулярным, а диагональным. Получается, что cкорость лодки должна быть направлена под тупым углом (π/2 + α) к направлению скорости течения и, следовательно, к берегу, от которого лодка движется, т.к. течение реки происходит параллельно этому берегу. Сделаем расклад скорости лодки на вертикальную составляющую и горизонтальную составляющую. У нас получится прямоугольный треугольник, в котором гипотенуза - это скорость лодки относительно воды v, катет, параллельный берегу, - скорость течения v', и катет, перпендикулярный берегу, - скорость лодки относительно берега V. Угол β - острый угол между скоростью v и берегом, который нам и нужно будет найти. Выходит, что скорость относительно берега равна геометрической разности скорости относительно воды и скорости течения:
V² = v² - v'² = 5² - 3² = 25 - 9 = 16 => V = 4 м/с.
Найдём время:
t = L/V = 200/4 = 50 c
Найдём угол β между направлением скорости лодки v и берегом из соотношения катетов прямоугольного треугольника - поделим скорость V (противолежащий катет) на скорость v' (прилежащий катет):
tgβ = V/v' = 4/3 - теперь найдём арктангенс: β = arctg(4/3) = 59,033 = 59°
Остаётся найти перемещение лодки относительно воды. Т.к. горизонтальная составляющая скорости лодки относительно воды v по модулю равна скорости течения v', то абсолютная скорость лодки в системе отсчёта "вода" равна этой же скорости:
Vabs = |v'| = v' = 3 м/с
За время t лодка переместится относительно воды по горизонтали на расстояние:
D = Vabs*t = 3*50 = 150 м
По вертикали лодка переместится на расстояние L, тогда полное перемещение лодки s будет равно геометрической сумме L и D:
s² = L² + D² = 200² + 150² = 40000 + 22500 = 62500 => s = √62500 = 250 м
ответ: 4 м/с, 50 с, 59°, 250 м.
Объяснение:
№1
Дано:
а=60 см; в=40 см; h=10 см; h2=1,5 м; p(плотность)=1600кг/м3; g=9,8H/кг
А=?
Си:
0,6 м; 0,4 м; 0,1 м
Формулы:
А=Fh2; F=mg; m=pV; V=авh
V=0,6м*0,4м*0,1м=0,024м3
m=1600кг/м3*0,024м3=38,4кг
F=38,4кг*9,8Н/кг=384Н
А=384Н*1,5м=576Дж
ответ: 576Дж
№2
Дано:
t=20 мин; S=30км; F=2,4кН
N=?
Си:
1200 сек; 30000 м; 2400Н
Формулы:
N=A/t
A=FS
А=2400Н*30000м=72000000Дж
N=72000000Дж/1200сек=60000Вт=60МВт
ответ: 60 МВт
№3
Дано:
m=0,5кг; V=10м/с
Ек=?
Формулы:
Ек=mV^2/2
^2V=v*v
v^2=10м/с*10м/с=100м^2/c^2
Ек=0,5кг*100м^2/c^2/2=25Дж
ответ: 25Дж
№4
Дано:
Еп=12Дж; m=0,4кг; g=9,8м/с2
h=?
Формулы:
h=Еп/mg
h=12дж/0,4кг*10м/с2=3м
ответ: 3м
№5
Дано:
m=300г; Ек=30Дж
V=?
Си:
0,3кг
Формулы:
V=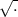 2Ек/m
2Ек/m
V=2*30Дж/0,3кг=14,14м/с
ответ: 14,14м/с