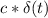Задание 5. Рассмотрите рисунок. Найдите величину силы, действующую справа от оси вращения рычага. (Масштаб одного деления равен 0,1м.) Дано: dı= В d= mj=5кг g=10, F F,-? Анализ: Решение: ответ:
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем.
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем.
Интересная задача
Дано:
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем.
Интересная задача
Дано:
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем.