Залежність від часу координати точки, яка рухається, має вигляд х=4+5t-2t2 . Визначте початкову координату, початкову швидкість і прискорення точки. Знайдіть переміщення за 2с. Побудуйте графік залежності швидкості від часу.

Показать ответ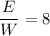

Ответ:

dashasapleva6

26.05.2020 23:09

ответ: $\dfrac{E}{W} = 8$

Объяснение:

Запишем уравнение гармонических колебаний в общем виде:

$x(t) = A \sin ( \omega t + \phi_{0})$

Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.

Отсюда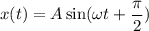 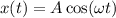$x(t) = A \sin ( \omega t +\dfrac{\pi }{2} )$ ⇒ $x(t) = A \cos ( \omega t)$ (1)

Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.

То-есть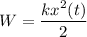 $W=\dfrac{kx^{2}(t) }{2}$ , но согласно уравнению (1) получим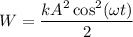 $W=\dfrac{kA^{2} \cos^{2} ( \omega t)}{2}\\$

Аналогично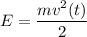 $E = \dfrac{mv^{2}(t) }{2}$ , однако мы знаем, что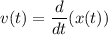 $v(t) =\dfrac{d}{dt} (x(t))$

Тогда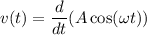 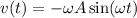$v(t) =\dfrac{d}{dt} ( A \cos ( \omega t))$ ⇒ $v(t) =-\omega A \sin( \omega t)$ , а это значит что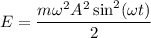 $E = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{2}$

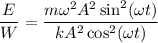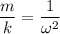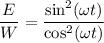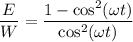Поэтому $\dfrac{E}{W} = \dfrac{m\omega^{2} A^{2} \sin^{2} ( \omega t)}{kA^{2} \cos^{2} ( \omega t)}\\}$ , так как $\dfrac{m}{k} = \dfrac{1}{\omega^{2} }$ , то $\dfrac{E}{W} = \dfrac{\sin^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ ⇒ $\dfrac{E}{W} = \dfrac{1 - \cos^{2} ( \omega t)}{\cos^{2} ( \omega t)}\\}$ (2)

Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)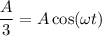 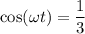$\dfrac{A}{3} = A \cos ( \omega t)$ ⇒ $\cos ( \omega t) = \dfrac{1}{3}$ , следовательно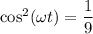 $\cos^{2} ( \omega t) = \dfrac{1}{9}$

Возвращаясь к уравнению (2) получим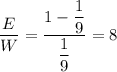 $\dfrac{E}{W} = \dfrac{1 - \dfrac{1}{9} }{\dfrac{1}{9} }} = 8$

0,0(0 оценок)

Ответ:

leeJLZeel

03.05.2020 03:19

Такая программа, разработанная в нашей стране, получила название алгоритма решения изобретательских задач (АРИЗ). Первые модификации АРИЗ появились еще в 40-х годах; с тех пор АРИЗ систематически совершенствовался, и нынешний АРИЗ-77 работает вполне надежно.

АРИЗ делит процесс решения задачи на семь этапов (частей). Каждый этап осуществляется постепенно - по шагам. "Лестница" АРИЗ имеет и "перила" - правила выполнения шагов. Если нарушено то или иное правило, через 2-3 шага ошибка становится явной: формулировки "не стыкуются". АРИЗ снабжен обширным фондом сжатой, спрессованной информации, полученной путем анализа десятков тысяч патентных описаний.

У нас нет возможности привести здесь полный текст АРИЗ-77, мы рассмотрим только один его фрагмент. Но сначала несколько предварительных пояснений. Известно, что правильно поставить задачу - значит наполовину ее решить. Обычно же приходится иметь дело с задачей "сырой", нечетко или вовсе неверно сформулированной. Поэтому, в сущности, процесс нахождения решения в значительной мере состоит в том, чтобы переосмыслить и изменить ее условия, ясно представить себе конечную цель. "Сырая" задача (ее называют ситуацией) содержит лишь указание на ту или иную техническую систему (или часть системы) и присущий этой системе недостаток. Одна и та же ситуация может быть превращена в множество различных задач. Возьмем, например, такую ситуацию: "Парусные суда передвигаются с малой скоростью. Как быть?" Эту ситуацию можно перевести в ряд задач: как улучшить парусное оснащение, как уменьшить сопротивление воды, как вообще обойтись без парусов и т. д. При работе методом проб и ошибок мысль стихийно перескакивает от одной задачи к другой. А бывает и хуже: выбрав одну задачу, человек упорно перебирает вариант за вариантом, не замечая, что взята не та задача. В АРИЗ есть надежные правила перехода от ситуации к задаче. В частности, каждая ситуация сначала должна быть переведена в мини-задачу по принципу: все остается без изменений, но исчезает тот отрицательный фактор, который указан в ситуации (или появляется требуемый положительный фактор). Если даже ситуация относится к безнадежно устаревшей технической системе, все равно сначала целесообразно рассмотреть мини-задачу. На замену технической системы неизбежно уйдут многие годы, поэтому полезно иметь пусть частичное, временное, но легко внедряемое решение. А решение мини-задачи всегда легко внедрить: это предопределено самой сутью мини-задачи (ничего нельзя менять).

Объяснение:

0,0(0 оценок)

Популярные вопросы: Физика