Замочіть у мильній воді дротяну рамку і у відбитому світлі розгляньте поверхню плівки. Поясніть явищн.

Показать ответ

Ответ:

anastasiya264

04.09.2020 00:49

Найти: E, φ

Дано:

m=2⋅10−4кг

l=0,5м

∠AOB=90∘

ε=1

g=10м/с2

k=14πε0ε=9⋅109ф/м

На каждый из зарядов (см. рисунок) действуют три силы: сила тяжести - mg→ ; сила натяжения нити - T⃗ и сила Кулона - F⃗ . Поскольку система зарядов находится в равновесии - геометрическая сумма сил равна нулевому вектору

mg→+T⃗ +F⃗ =0

спроецируем это равенство на оси координат с учетом того, что α=45∘ и cosα=sinα

x: Tcosα=mg

y: Tcosα=F=kq2l2

q=mgl2k−−−−−√

E⃗ =E⃗ 1+E⃗ 2

E1=E2=kql2=kmgl2−−−−√

E=2kmgl2−−−−−√

φ=2φ1=2kql=2kmg−−−−√

Объяснение:

0,0(0 оценок)

Ответ:

настяWebStorage

22.10.2022 20:00

Рассмотрим два случая.

1. На шарик действует лишь сила со стороны электрического поля, а сила тяжести не действует.

Силу рассчитаем, как произведение эл. заряда на напряженность поля:

F = Eq

Далее найдем ускорение, с которым этот шарик двигался бы в электрическом поле, не будь он подвешен на нити:

а = F/m (по второму закону Ньютона)

Теперь воспользуемся формулой для определения периода колебаний нитяного маятника в однородном гравитационном поле:

$T = 2\pi \sqrt{\frac{l}{g} }$

Только вместо ускорения свободного падения g, используем ускорение a, рассчитанное нами ранее. Получим формулу:

$T = 2\pi \sqrt{\frac{l}{a} }$ или с учетом ранее проведенных выкладок:

$T = 2\pi \sqrt{\frac{lm}{Eq} }$

Здесь, напоминаю, l - длина нити

Расчёт: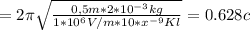 $Т = 2\pi \sqrt{\frac{0,5 m*2*10^{-3}kg} {1*10^{6}V/m*10* x^{-9}Kl} } = 0.628 c$

2. Если на тело действует дополнительно сила тяжести, сообщающая ему ускорение свободного падения g = 9,8 м/с². Всё то же самое, только вместо ускорения a в формуле будет ускорение (a+g)

$T = 2\pi \sqrt{\frac{l}{a+g} }$