Заряджене тіло, розмірами якого можна знехтувати порівняно з відстанями від нього до інших заряджених тіл, що розглядаються. a. матеріальна точка; б. заряджена точка; B. точковий заряд; г. точковий струм.
Решение Разобьем нить на бесконечно малые участки dl . Тогда находящиеся на них заряды равны: dq dl (1) Где – линейная плотность. Эти заряды можно рассматривать как точечные. Эти равные по величине заряды расположены симметрично относительно оси симметрии нити и равноудалены от точки O. Поэтому dE1 dE2 и проекции векторов напряженности E1 d и dE2 на ось Оx компенсируют друг друга. Следовательно, вектор dE напряженности электрического поля от каждого элементарного заряда направлен вдоль оси Oy и его модуль равен: cos 4 1 cos 2 0 1 a dl dEy dE (2)
На подвижной блок действуют три силы: сила F - это сила, приложенная к свободному концу верёвки; вес P и сила тяжести g тянут блок вниз (рисунок 1).Для решения задачи используем момент силы. Это физическая величина - М (В СИ измеряется Ньютон на метр), которая равна произведению модуля силы F (В СИ измеряется в Ньютонах) на её плечо l (В СИ измеряется в метрах):
3. Дополним схему (рисунок 2): A и B - точки вращения блока, а точка О - центр вращения, R - радиус подвижного блока. А значит AO=OB=R. И стрелочками обозначим направление движения блока (-, + ) для верного определения действующих сил.
4. Рассмотрим сумму моментов сил относительно точки А (рисунок 2):
Первый момент силы - это вес Р надо умножить на длину рычага , то есть длину АО, которая согласно рисунку равна R :
Сила Р будет вращать блок за часовой стрелкой, то есть в отрицательном направлении.
Второй момент силы - это силу тяжести g надо умножить на длину рычага , то есть длину АО, которая согласно рисунку равна R :
Сила mg также будет вращать блок за часовой стрелкой, то есть в отрицательном направлении.
Третий момент силы - это силу F, приложенную к концу верёвки надо умножить на длину рычага , то есть длину АB, которая равна 2R :
Сила F будет вращать блок против часовой стрелки, то есть в положительном направлении.
5. Учитывая направления действий сил, сложим все моменты сил и прировняем эту сумму к нулю, поскольку система находится в состоянии равновесия:
6. Подставляем вместо буквенные значения с формул моментов сил:
7. Выполним математические превращения для получения формулы веса ведра со смолой:
8. Подставляем исходные данные задачи в полученную формулу, а значение g как постоянной величины берем равное 10м/с²:
Масса ведра со смолой 34,5 кг
Объяснение:
На подвижной блок действуют три силы: сила F - это сила, приложенная к свободному концу верёвки; вес P и сила тяжести g тянут блок вниз (рисунок 1).Для решения задачи используем момент силы. Это физическая величина - М (В СИ измеряется Ньютон на метр), которая равна произведению модуля силы F (В СИ измеряется в Ньютонах) на её плечо l (В СИ измеряется в метрах):3. Дополним схему (рисунок 2): A и B - точки вращения блока, а точка О - центр вращения, R - радиус подвижного блока. А значит AO=OB=R. И стрелочками обозначим направление движения блока (-, + ) для верного определения действующих сил.
4. Рассмотрим сумму моментов сил относительно точки А (рисунок 2):
Первый момент силы - это вес Р надо умножить на длину рычага , то есть длину АО, которая согласно рисунку равна R :Сила Р будет вращать блок за часовой стрелкой, то есть в отрицательном направлении.
Второй момент силы - это силу тяжести g надо умножить на длину рычага , то есть длину АО, которая согласно рисунку равна R :Сила mg также будет вращать блок за часовой стрелкой, то есть в отрицательном направлении.
Третий момент силы - это силу F, приложенную к концу верёвки надо умножить на длину рычага , то есть длину АB, которая равна 2R :Сила F будет вращать блок против часовой стрелки, то есть в положительном направлении.
5. Учитывая направления действий сил, сложим все моменты сил и прировняем эту сумму к нулю, поскольку система находится в состоянии равновесия:
6. Подставляем вместо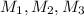
буквенные значения с формул моментов сил:
7. Выполним математические превращения для получения формулы веса ведра со смолой:
8. Подставляем исходные данные задачи в полученную формулу, а значение g как постоянной величины берем равное 10м/с²:
ответ: 34,5 кг