Зчас при рівномірному прямолінійному русі визначають за формулою
а. t = suб. т= s/u b. t = shu г. t = u/s
4 зміну з часом положення тіла в просторі називають
a. траекторією б. механічним рухом b. пройденим шляхом г. переміщенням
5 переміщення тіла при русі по колу за півперіоду рівне
а. радіусу б. діаметру в. довжині кола г. нулю
6 частота обертання вала токарного станка 3000 об/хв. знайти період обертання
вала,
7 які частини рухомого трактора нерухомі відносно кабіни?
а. руль та фари б. колеса та фари b. поршні двигуна г. двигун та рама
8 колесо радіусом r котиться без просковзування по дорозі. на яку відстань воно
переміститься, якщо зробить два оберти?
а. 2r b. 2пr б. 4rtr г., 4r
9 при підйомі на гору лижник пройшов 300 м, рухаючись зі швидкістю 0,8 м/с. 3
гори він
спустився за 25 с. яка середня швидкість лижника на всьому шляху?
10 період коливань пружинного маятника залежить від
а. маси тіла та жорсткості пружини б. маси тіла та довжини пружини
b. розмірів маятника г. від матеріалу пружини та об'єму тіла
11 на графіку вкажіть швидкості руху велосипедиста
1, км

Показать ответ

Ответ:

Артём84748

16.06.2020 10:48

$S=S_{1}+S_{2}+S_{3} =18,75+150+30=198,75$ м.

Объяснение:

Дано:

V=27 км/ч =7,5 м/с - скорость автобуса на втором участке пути;

$t_{1} =5$ с - время, за которое автобус разогнался до скорости, равной 27 км/ч;

$t_{2} =20$ с - время движения автобуса с постоянной скоростью, равной 27 км/ч;

$t_{3} =8$ с - время торможения автобуса, то есть уменьшения скорости от 27 км/ч до 0.

Необходимо найти: .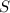

Как видно из задачи, общий путь между остановками будет равен пути, потраченном на разгон, пути с постоянной скоростью и пути, с постоянным торможением. Разберем каждый участок пути отдельно.

Путь на первом участке, согласно формуле движения с постоянным ускорением будет иметь вид:

$S_{1} =V_{0} *t+\frac{a_{1}*t_{1} ^2}{2}$

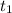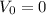Время $t_{1}$ нам известно, неизвестно лишь ускорение . Так как начальная скорость $V_{0} =0$ м/с, то можем записать:

$S_{1} =\frac{a_{1}*t_{1}^2 }{2}$ (1)

Ускорение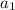 $a_{1}$ в данном случае будет иметь вид: 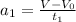$a_{1}=\frac{V-V_{0}}{t_{1} }$ , и если 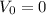$V_{0} =0$ , то получаем: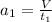 $a_{1}=\frac{V}{t_{1} }$

Подставляя в формулу (1) получим:

$S_{1} =\frac{\frac{V}{t_{1} }*t_{1}^2 }{2}= \frac{V*t_{1} }{2}$

Можем сразу посчитать:

$S_{1} =\frac{7,5*5}{2}=18,75$ м. - пройдя расстояние автобус разгонится до скорости 27 км/ч или 7,5 м/с за 5 секунд.

Вторая часть пути, это путь с постоянной скоростью .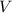

На данном участке пути, пройденное расстояние будет иметь вид:

$S_{2} =V*t_{2}=7,5*20=150$ м. - такое расстояние проедет автобус с постоянной скоростью.

Затем, автобус станет тормозить, то есть у нас равнозамедленное движение с постоянным отрицательным ускорением.

Пройденный путь на данном участке будет, согласно формуле равнозамедленного движения:

$S_{3}=V*t_{3}+\frac{a_{2}*t_{3}^2}{2}$ (2)

В данном случае, так как автобус в итоге затормозит и уменьшит свою скорость до нуля (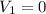 $V_{1}=0$ ), то ускорение можно найти согласно формуле:

$V_{1}-V=a_{2}*t_{3}\\$

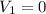Если $V_{1}=0$ м/с, то ускорение будет равно:

$a_{2}=\frac{V_{1}-V}{t_{3}}$ (3)

Тогда подставляя формулу (3) в формулу (2) получим:

$S_{3} =V*t_{3} +\frac{\frac{V_{1} -V}{t_{3}}*t_{3}^2}{2}=V*t_{3} +\frac{(V_{1}-V)*t_{3} }{2}$

Все данные нам известны, подставляем и считаем:

$S_{3} =V*t_{3} +\frac{(V_{1}-V)*t_{3} }{2} =7,5*8+\frac{(0-7,5)*8}{2}=60+\frac{-60}{2}=60-30=30$ м. - за такое расстояние автобус полностью остановится со скорости 7,5 м/с за время 8 с.

Теперь, чтобы найти весь путь, пройденный автобусом, сложим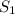 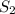$S_{1}$ , $S_{2}$ и $S_{3}$ :

$S=S_{1}+S_{2}+S_{3} =18,75+150+30=198,75$ м.

0,0(0 оценок)

Ответ:

razdor1996Rqzdor

12.04.2022 10:46

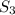Дано:

m = 1,3 кг

L = 4 м

L₁ = 5 м

L₂ = 3 м

g = 10 м/с²

T₁, T₂ - ?

При данных значениях длин стержень и нити будут образовывать прямоугольный треугольник, т.к. точка подвеса располагается точно на линии действия силы тяжести (см. рисунок).

Стержень находится в равновесии. Воспользуемся одним из условий равновесия - равенством моментов сил, действующих на стержень. На стержень действуют три силы: сила тяжести mg, сила натяжения длинной нити T₁ и сила натяжения короткой нити T₂. Момент силы - это произведение силы F и плеча d, где плечо d - это кратчайшее расстояние между точкой опоры и линией действия силы:

M = F*d

Для того, чтобы найти какую-либо из сил натяжения, мы будем рассматривать равенство моментов сил относительно точек А и B.

ТОЧКА А.

M + M₁ + M₂ = 0 - векторная сумма

-M + 0 + M₂ = 0 - алгебраическая сумма, где

-M = -mg*d - знак минуса стоит потому, что сила тяжести стремится повернуть стержень по часовой стрелке относительно точки А.

M₁ = T₁*d₁(A) = 0, т.к. сила T₁ не стремится повернуть стержень относительно точки, к которой она и приложена. Другими словами - плечо силы T₁ относительно точки А равно нулю (d₁(A) = 0), поэтому момент этой силы равен нулю.

M₂ = T₂*d₂ = T₂*L - знак плюса стоит потому, что сила натяжения T₂ стремится повернуть стержень против часовой стрелки относительно точки А.

Выходит, что:

M₂ = M

T₂*L = mg*d

Мы не знаем плечо d. Но его можно выразить путём геометрических соображений. Обратимся к рисунку. Плечо d равно стороне АС прямоугольного треугольника ABC. Этот треугольник подобен прямоугольному треугольнику A'B'C' по трём углам (углы B и B' являются вертикальными, а углы А и А' - взаимно перпендикулярными, углы С и С' - прямые). Если поделим АB на AC, то получим коэффициент подобия, который точно также можно получить, поделив А'B' на A'C':

AB/AC = А'B'/A'C'

АB = L/2, AC = d

A'C' = L₂, A'B' = √(A'C'² + B'C'²) - по теореме Пифагора, B'C' = AB = L/2 =>

=> A'B' = √(L₂² + (L/2)²) = √(L₂² + L²/4), тогда:

(L/2) / d = √(L₂² + L²/4) / L₂ - выражаем d:

d = (L/2) : (√(L₂² + L²/4) / L₂) = (L/2)*L₂/√(L₂² + L²/4) = L*L₂ / 2√(L₂² + L²/4)

Подставляем в уравнение моментов:

T₂*L = mg*d

T₂*L = mg*L*L₂ / 2√(L₂² + L²/4) - делим обе части на L:

T₂ = mg*L₂ / 2√(L₂² + L²/4) = 1,3*10*3 / 2√(3² + 4²/4) = 39 / 2√13 = 13*3 / 2√13 = √13*3/2 = √13*1,5 = 5,4083... = 5,4 Н

ТОЧКА B.

M + M₁ + M₂ = 0 - векторная сумма

M - M₁ + 0 = 0 - алгебраическая сумма, где

M = mg*d

-M₁ = -T₁*d₁, получается:

M = M₁

mg*d = T₁*d₁

Плечо d мы уже выразили. Остаётся выразить плечо d₁. Мы можем выразить d₁, используя два прямоугольных треугольника: АDC' и A'DC'. Выразим плечо из теоремы Пифагора, обозначив сторону A'D через x:

АDC': d₁² = L² - (L₁ - x)²

A'DC': d₁² = L₂² - x²

Приравняем, чтобы выразить х:

L² - (L₁ - x)² = L₂² - x²

L² - (L₁² - 2*L₁*x + x²) = L₂² - x²

L² - L₁² + 2*L₁*x - x² = L₂² - x²

L² - L₁² + 2*L₁*x = L₂²

2*L₁*x = L₂² - L² + L₁²

x = (L₂² - L² + L₁²) / 2L₁ = (3² - 4² + 5²) / (2*5) = (9 - 16 + 25)/10 = 18/10 = 1,8 м

Тогда:

d₁² = L₂² - x² => d₁ = √(L₂² - x²)

Выражаем T₁ из уравнения моментов: