Железнодорожный состав начинает двигаться из состояния покоя. А) Каково ускорение движения состава, если за 3Зс он сместился на 9м.
Б) Каковы максимальная и средняя скорости движения состава на этом участке.
В) Напишите уравнения зависимости координаты и скорости от времени для состава х=х (t) и V=V(t). Постройте графики движения и скорости состава.
г) После того, как поезд набирает максимальную скорость, от него отцепляют последний вагон, который через некоторое время останавливается. Как будут относиться пути, пройденные составом и последним вагоном до момента остановки вагона? Состав движется равномерно с максимальной скоростью.

Показать ответ

Ответ:

динани1

06.10.2021 13:40

ответ: m≈ 6,7*10^-27 кг.

Объяснение: По условию дано, что q (т.е.заряд) равен 2*e (где е - это элементарная частица). Тогда q= 2*|1,6*10^-19|Кл= 3,2*10^-19 Кл.

Как помнится, что работа электрического тока высчитывается по формуле: A= q*U. Значит считаем работу, A= (3,2*10^-19)Кл * 105 В= 3,36*10^-17 Дж. В данном случае, A=K (кинетическая энергия, т.к V1=0, а V2=1,0*10⁵м/с). K=m*V²/2, то из этой формулы выражаем m= 2*А/V²= (2*3,36*10^-17Дж)/(1,0*10⁵ м/с)= 6,72*10^-27 кг≈6,7*10^-27 кг. Если что-то следует объяснить более подробно, обращайся!

0,0(0 оценок)

Ответ:

rustikkhusnutdi

22.10.2020 03:45

Дано:

q₁ = q₂ = q₃ = q₄ = Q = 10⁻⁷ Кл

Найти: q₀

Изобразим графически все заряды. Заряды в вершинах квадрата пронумеруем от 1 до 4, заряду в центре квадрата присвоим номер 0.

Если система находится в равновесии, то векторная сумма сил, действующих на каждый из зарядов равна 0. Заметим, что поскольку картинка симметрична относительно центрального заряда, то выбирать его для рассмотрения смысла нет. Выберем для рассмотрения один из зарядов, расположенных в вершинах квадрата, например, № 4.

Запишем:

$\vec{F_{41}}+\vec{F_{42}}+\vec{F_{43}}+\vec{F_{40}}=\vec{0}$

Введем ось, на которую спроецируем эти силы. Удобно направить эту ось вдоль диагонали квадрата. Тогда, получим:

$F_{41}\cos\alpha+F_{42}+F_{43}\cos\alpha -F_{40}=0$

$F_{40}=F_{41}\cos\alpha +F_{42}+F_{43}\cos\alpha$

Введенный угол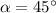 $\alpha =45^\circ$ , так как диагональ квадрата делит его на два равных равнобедренных прямоугольных треугольника.

Подставляя значение косинуса этого угла и расписывая силы Кулона, получим:

$k\dfrac{|q_4||q_0|}{\left(\frac{a\sqrt{2} }{2} \right)^2}=k\dfrac{|q_4||q_1|}{a^2}\cdot\dfrac{\sqrt{2} }{2} +k\dfrac{|q_4||q_2|}{(a\sqrt{2}) ^2}+k\dfrac{|q_4||q_3|}{a^2}\cdot\dfrac{\sqrt{2} }{2}$