1. 1) Какими свойствами обладает диаметр, перпендикулярный хорде? 2) Может ли хорда окружности быть больше диаметра?
3) Может ли серединный перпендикуляр хорды не быть диаметром?
2. Начертите окружность и проведите два перпендикулярных друг
другу Диаметра AB и CD. Найдите градусные меры дуг, на которые
делят окружность точки A, B, C и D.
3. Найдите расстояние от центра окружности до хорды, если хорда
длиной 8 cm стягивает дугу в 90°.
1. Из данной точки окружности проведены две хорды, равные
радиусу окружности. Найдите угол между ними.
5. Из данной точки окружности проведены диаметр и хорда, равная
радиусу окружности. Найдите угол между ними (рис. 4).
Пусть AC - большая диагональ ромба; AC = d и острый угол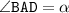
. Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и в точке пересечения делятся пополам.
Из прямоугольного треугольника AOD: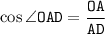
отсюда выразим AD: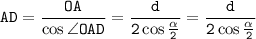 
Площадь ромба равна S = a*h, с другой стороны: S = a²*sinα, приравнивая площади, получим h = a * sin α, где а - сторона ромба.
Высота ромба является диаметром вписанной окружности в ромб, тогда радиус вписанной окружности равен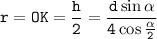
Рассмотрим теперь прямоугольный треугольник SOK и найдем в нем SK - апофему пирамиды: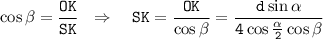
Найдем теперь площадь боковой поверхности пирамиды
Сначало строишь прямой угол , далее проводишь биссектрису с циркуля :
1)построй прямой угол (думаю что сможешь это сделать )
2) выбрать произвольный раствор циркуля
3) иглу циркуля ставишь на сам угол
4) проведи дугу которая пересекает стороны угла
5) из точек касания дуги со сторонами угла не меняя раствор циркуля проведи дуги
6) пусть точка касания двух последних дуг будет называться K
7) соедини точку (в моем случае B с точкой K)
Теперь мы имее два угла по 45 градусов
С верхнего (ABO у меня) угла равного 45 градусам также проведи биссектрису в итоге 45/2=22°30' , наш нижний угол равен 45°
в итоге ( у меня угол LBC) равен 22°30'+45°=67°30'