1.24. В треугольник ABC на рисунке 13 вписана окружность. Точки касания окружности и Z делят стороны треугольника AB и AC на отрезки, раз-
ности которых равны 3 см и 4 см соответственно (AN - NB, AZ > ZC).
Найдите стороны треугольника, если его периметр равен 28 см.
Объяснение:
1) MN-средняя линия. По т. о средней линии MN=0,5АС, MN=9.
2)MN-средняя линия. По т. о средней линии MN||АС.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Значит ΔВMN подобен ΔВАС по двум углам.Коэфициент подобия к=1/2
Т.К. отношение периметров подобных треугольников равно коэффициенту подобия , то Р(ΔВMN)/Р(ΔВАС)=к, Р(ΔВMN)/16=1/2, Р(ΔВMN)=8.
Т.К.отношение площадей подобных треугольников равно квадрату коэффициента подобия, то S(ΔВMN)/S(ΔВАС)=к²,
16/S(ΔВАС)=1/4, S(ΔВАС)=64
Пусть дана равнобедренная трапеция с диагоналями
с диагоналями 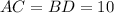 см и
см и 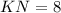 см — медиана (см. вложение).
см — медиана (см. вложение).
Сделаем дополнительное построение: проведем прямую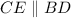 . Образовался равнобедренный треугольник
. Образовался равнобедренный треугольник 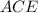 с боковыми сторонами
с боковыми сторонами 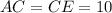 см, равновеликий с трапецией
см, равновеликий с трапецией 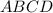 (так как треугольники
(так как треугольники 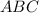 и
и 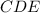 равны по третьему признаку равенства треугольников). Следовательно, средние линии
равны по третьему признаку равенства треугольников). Следовательно, средние линии 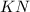 и
и 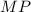 тоже равны (средние линии
тоже равны (средние линии 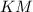 и
и 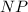 соответственно равны треугольникам
соответственно равны треугольникам 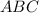 и
и 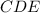 ).
).
Рассмотрим равнобедренный треугольник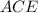 . Так как
. Так как 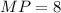 см — его средняя линия, то
см — его средняя линия, то 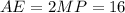 см. Опустим перпендикуляр
см. Опустим перпендикуляр 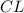 — высота, биссектриса и медиана. Значит,
— высота, биссектриса и медиана. Значит, 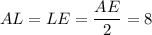 см.
см.
Рассмотрим прямоугольный треугольник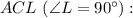
По теореме Пифагора: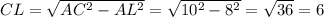 см.
см.
Следовательно, площадь треугольника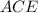 составляет
составляет 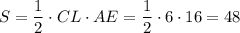 см².
см².
Так как треугольник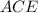 и трапеция
и трапеция 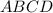 равновеликие, то площадь трапеции равна 48 см².
равновеликие, то площадь трапеции равна 48 см².
ответ: 48 см².