1. биссектриса угла b параллелограмма abcd делит сторону ad на два отрезка ak и kd так, что ak-kd=1 см. найдите стороны параллелограмма, если его периметр равен 40 см 2. в равно бедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60 градусов. найдите меньшее основание. 3. в равнобокой трапеции диагональ является биссектрисой тупого угла, а её основы равны 10 см и 6 см. найдите периметр трапеции. 4. точки a и b лежат по одну сторону от прямой l. расстояние до неё от точки a равно 7 см, а от точки m, которая является серединой ab - 5 см. найдите расстояние от точки b до прямой l.

ответ:1. 50°

2. 30°

3.75°

Объяснение: Смотри, в равнобедренном треугольнике углы при основании равны. Также, в любом треугольнике сумма всех трех углов равна 180°. Всегда)

Далее, в третьем случае один из углов равен 30°. Делаем вывод что 180-30=150° (два оставшихся угла), и потом 150/2=75° (один углом при основании)

Во втором случае: угол равен 120°. Вычитаем из 180-120=60° (два оставшихся ушла при основании), и 60/2=30° (один угол пр основании).

И в первом случае угол равен 80°. Вычитаем 180-80=100° (два угла при основании), и 100/2=50° (один угол пр основании).

234

Объяснение:

Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.

Угол BDA равен углу DBC как накрестлежащий. Следовательно  CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.

Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.

Нужно найти катет HD.

Используем формулу для нахождения гипотенузы в прямоугольном треугольнике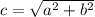

Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.

Найдем площадь трапеции по формуле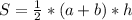

S=1/2*(15+24)*12=6*39=234