1. Будет ли отрезок AD пересекать прямую или нет, если отрезки AB, BC и CT пересекают ее? 2. А в случае, когда отрезки AC и BC пересекают данную прямую, но не пересенсанот BD? 3. А если AB и CD пересекают данную прямую, но не пересекают BC. 4. А если AB и CD не пересекают данную прямую, но пересекают все 5. Что можно сказать об отрезке AD, если AB, BC и CD не пересекают данную прямую? 6. Что можно сказать об отрезке AD, если и AB, и BC, и CD не пересекают данную прямую? Запишите ваши ответы, а затем обоснуйте их на чертеже.

Объяснение:

1. Средние линии треугольника равны половинам сторон, которым они параллельны. Средние линии равны 6, 9 и 10 см.

Значит, стороны равны 12, 18 и 20 см.

Периметр P = 12 + 18 + 20 = 50 см.

2. Средняя линия трапеции равна половине суммы ее сторон.

Стороны относятся как 3:5, обозначим их 3x и 5x.

(3x + 5x) : 2 = 32

8x : 2 = 32

x = 8

Основания равны 3*8 = 24 см и 5*8 = 40 см.

3. Вписанная окружность делит основания трапеции на такие же отрезки, как и боковые стороны.

То есть, если окружность делит одну сторону на x см и (7-x) см, а другую сторону на y см и (12-y) см, то основания будут такие:

Одно: x + y, а второе: (7-x) + (12-y) = 19 - x - y.

Периметр P = 7 + 12 + x + y + 19 - x - y = 19 + 19 = 38 см.

Дальше сами, у вас слишком много задач в одном вопросе.

N 8:

Для начала найдем площадь более темно закрашенной фигуры:

воспользуемся формулой площади треугольника S =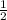 × a × b × sin ∠(a,b)

S =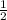 × 12 × 12 × sin 120° = 36√3 см²

Теперь площадь менее темно закрашенной фигуры:

воспользуемся формулой площади сектора S = π × R² ×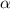 / 360°, а потом отнимем от полученной площади площадь более темно закрашенной фигуры:

S = π × 12² × 120° / 360° - 36√3 = 48π - 36√3 см² (не был уверен что нужно подставлять значение числа π, ведь об этом ничего не сказано)

N 9:

Для начала найдем диаметр по формуле длинны отрезка по координатам: √((х₁ - х₂)² + (y₁ - y₂)²)

d = √136 = 2√34, тогда R = √34

Далее по формуле площади круга решаем: S =  π × R² = 34π