1.Даны точки А(2;1;-4),В(4;0;-2) , С (0;-3;-0) Вычислите угол между векторами АВ и АС
2. Запишите уравнение плоскости проходящей через точку А(1;2;3) и вектор
нормали n(2;1;4)
3. Составьте уравнение прямой проходящей через точки А(-2;0;2) В(4;1;2)
4.По уравнению сферы определите координаты центра сферы и радиус
(х-3) 2 +(у+6) 2 +z 2 =64

Показать ответ

Ответ:

ТинкиВинкиДанки

04.02.2022 09:34

sin=прот.ст./гипот

sinA=BC/AB=4/5=0,8

sinB=AC/AB=3/5=0,6

cos=прил.ст./гипот.

соsA=AC/AB=3/5=0,6

cosB=BC/AB=4/5=0,8

tg=прот.ст./прил.ст.

tgA=BC/AC=4/3=1 1/3

tgB=AC/BC=3/4=0,75

ctg=прил.ст./прот.ст.

ctgA=AC/BC=0,75

ctgB=1 1/3

Смотря как ты начертишь треугольник. Если ОМ будет лежать против угла в 30 градусов, то значит равна половине гипотенузы, 24/2=12

А если это другой из катетов, то находишь по теореме Пифагора

cos=прил.сторон./гипот.

sin=прот./гип.

один из катетов, который будет лежать против 30°, равен половине гипотенузы, 12/2=6, а другой по теореме Пифагора

а) 12²-6²=144-36=108

б) если треугольник прямоугольный и один из углов равен 45°, то значит он равнобедренный, 180°-(90°+45°)=45°

0,0(0 оценок)

Ответ:

данич36

21.04.2020 12:07

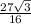
ответ: S= $\frac{27\sqrt{3} }{16}$

Объяснение:

треугольник с углами 30° и 120° -это равнобедренный треугольник))

две медианы равнобедренного треугольника (проведенные к боковым сторонам) равны... осталось найти медиану к основанию (m1) и медиану к боковой стороне (m2=m3)

составленный треугольник тоже получится равнобедренным...

его площадь можно найти по формуле Герона...

а можно найти (по теореме косинусов) косинус угла между медианами, найти (используя основное тригонометрическое тождество) синус этог угла и найти площадь по формуле S=0.5ab*sin(x)

$(\frac{3}{2} )^{2} =2*(\sqrt{\frac{63}{4} } )^{2} -2*\frac{63}{4} *cos(x)$