1. Диагональ BD1 прямоугольного параллелепипеда, равная 8см, составляет с плоскостью
АВСD угол в 30. AD =√11см. Найти ребро АВ.
2.В наклонной треугольной призме все боковые ребра равны. Боковое ребро наклонено к
плоскости основания под углом в 60. Высота призмы равна 10см. Найти длину бокового ребра.
3. В прямой призме ABCDA1B1C1D1 основанием является ромб, диагональ BD которого равна
10см, угол CAD =30, боковое ребро равно 12√3 см. Найти площадь прямоугольника АСС1А решить задачи с чертежом
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC ,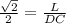
,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
И ΔВCD-равнобедренный ⇒ВD=DС=L√2.
Значит АВ=2L√2.
S=1/2*a*h , S(АВС)=1/2*2L√2*L√2=2L² .
1) ΔАВС - равнобедренный, АВ=ВС , АС - основание , ∠В=120°,
∠А=∠С = (180- 120)/2 = 30 °- углы при основании равны.
2) АН =8 см - высота к боковой стороне АВ ⇒∠Н=90°⇒
ΔАНС - прямоугольный , АС- гипотенуза , АН и НС - катеты.
Из пункта 1) ∠С=30°.
Сторона , лежащая напротив угла в 30° равна половине гипотенузы:
АН = АС/2 ⇒ АС= 2 * АН
АС = 2*8= 16 см
ответ: АС= 16 см - основание ΔАВС.
Объяснение:
Пусть дан рб треугольник АВС, с основанием АС.
СВ продлим вверх треугольника, тк высота АН =8 будет снаружи треугольника, тк АВС тупоугольный.
Рассмотрим Тр. АВН. Угол Н =90. внешний угол АВС=120 => угол НАВ=120-90=30.
Тогда НВ =половине АВ.
Пусть НВ=х, тогда АВ= 2х
Рассмотрим треугольники АВМ - ( ВМ - высота АВС к АС) и тр АВН.
АВ - общая,
Углы НАВ=ВАМ=30
Углы НВА=АВМ=60
=> треугольники равны => АМ =8 => АС=16.