1)две стороны треугольника равны 8 см и 6 см.высота,проверенная к первой стороне,равна 3 см .найдите высоту,проверенную ко второй стороне треугольника. 2)найдите площадь прямоугольного треугольника , в котором гипотенуза равна 5 см,а один из катеров равен 4 см.
32дм²
Объяснение:
Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S =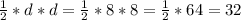 (дм²)
(дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
x² + x² = 8²
2x² = 64
x² = 32
x = √32 = √16*2 = 4√2 (дм)
Площадь квадрата x², то есть площадь равна 32дм²
Проведем высоту к основанию равнобедренного треугольника. Высота поделит основание на две равные части, т.е. 18/2=9.
Когда мы провели высоту (она же медиана, кстати), у нас образовалось два прямоугольных треугольника. Э ти треугольники будут равны, т.к. гипотенузы уних и катеты равны.
Площадь одного треугольника найдем по теореме Пифагора
41^2=9^2(половина основания большого треугольника)+x^2(х- высота)
х=40.
40 и 9 - катеты тр. S= половина произведения катетов (40*9)/2=180.
Т.к. прямоугольные тр. равны, то площадь большого треугольника равна: 2*180=360.
ответ:360!