1. Хорда делит окружность на две дуги, градусные меры которых пропорциональны числам 4 и 6. Чему равен угол, вписанный в данную окружность, сторонам которого принадлежат концы этой хорды?

Построение сечения: Назовем искомую плоскость MNK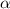 . Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью  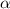, следовательно, линии пересечения параллельны. Значит,  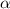пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.

Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.

поскольку это равнобедренный треугольник то его две стороны должны быть одинаковой длины

тоесть или 5 см и 5 см или 2 см и 2 см

рассмотрим эти два случая (фото)

за признаком треугольника :

Длина третьей стороны треугольника должна быть больше суммы двух других сторон, и не может быть и меньше разности двух других сторон

рассмотрим случай где две стороны 5 и одна 2

5-5<2<5+5

0 <2<10

....

5-2<5<5+2

3<5<7

неравенство верное,значит такой треугольник существует

--------------------------------

рассмотрим случай где две стороны 2 и одна 5

2-2<5<2+2

0<5<4

поскольку 5>4 то такого треугольника не существует

ОТВЕТ: ДВЕ СТОРОНЫ ТРЕУГОЛЬНИКА РАВНЫ 5 СМ И ТРЕТЬЯ 2 СМ