1. Изобразите два отрезка а и b, где а<b. При цир- куля и линейки: а) разделите отрезок і пополам; 2. H б) на произвольной прямой отложите отрезок, рав- ный а+ b; в) постройте отрезок, равный b - а.
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
см
Отношение площадей подобных треугольников равно квадрату отношения сходственных сторон.
см²
Площадь треугольника DFR можно вычислить так же по формуле:
7. Так как у треугольника равны две стороны,по определению он равнобедренный,значит,углы при основании равны.<А=<С=70
По теореме <В= 180 - 70 - 70 = 40
8. Так же,как и в предыдущей задаче доказывае , что треугольтреугольник р/б и два оставшихся угла равны. Обозначим каждый из них за х. Тогда по теореме о сумме углов треугольника 2х+50=180
2х=130
Х=65
<А=<С=665
9. Как и в двух задачах тр-к р/б и углы при основании равны. По свойству смежных углов <С=180-125 =55 =<А
<В по теореме о сумме углов треугольник равен 180 - 55 - 55 = 70
10.<В=180-140=40 по свойству смежных углов
АСВ-равнобедренный,поэтому <А=<С. Каждый из этих углов по теореме о сумме углов тр-ка = (180-40):2=70
11.по свойству смежных углов <С= 180-60-50=70. Продлим прямые АС и СД. <ВСД=60=<В как накрест лежащие углы по свойству параллельных прямых при параллельных АС И СД и секущей ВС. <А= 180 -60 - 70= 50
12.ADB-равнобедренный,<А=<АВД=30.
<АДВ=180-30-30=120
<ДВС=<С,тк тр-к ДВС равнобедренный.
По теореме о внешнем угле <ДСВ=<С=120÷2=60
<В по теореме о сумме углов тр-ка равен 180-60-30=90
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
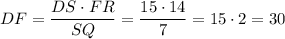 см
см
Отношение площадей подобных треугольников равно квадрату отношения сходственных сторон.Площадь треугольника DFR можно вычислить так же по формуле:
Из треугольника DFR по теореме косинусов:
DR² = 30² + 14² - 2 · 30 · 14 · 0,6
DR² = 900 + 196 - 504 = 592
DR = √592 = 4√37 см
Объяснение:
1.по теореме о сумме углов треугольника 180 - 35 - 45 = 100
2.по свойству смежных углов <А = 180 - 110 =70 . <С=180-70 - 40 =70
3.по свойству смежных углов <В=180 - 120 = 60, <С =180-110=70. По теоремео сумме < тр-ка <А=180 - 70 - 60 = 50
4. <С-прямой(90),180 - 90 - 30 =60 -<В
5.С снова равен 90,<В=180 - 130 = 50
аналогично другим задачам <А=180 - 90
-50 = 40
6.по свойству вертикальных углов <А=40
<В по теореме равен 180 - 40 - 105 = 35
7. Так как у треугольника равны две стороны,по определению он равнобедренный,значит,углы при основании равны.<А=<С=70
По теореме <В= 180 - 70 - 70 = 40
8. Так же,как и в предыдущей задаче доказывае , что треугольтреугольник р/б и два оставшихся угла равны. Обозначим каждый из них за х. Тогда по теореме о сумме углов треугольника 2х+50=180
2х=130
Х=65
<А=<С=665
9. Как и в двух задачах тр-к р/б и углы при основании равны. По свойству смежных углов <С=180-125 =55 =<А
<В по теореме о сумме углов треугольник равен 180 - 55 - 55 = 70
10.<В=180-140=40 по свойству смежных углов
АСВ-равнобедренный,поэтому <А=<С. Каждый из этих углов по теореме о сумме углов тр-ка = (180-40):2=70
11.по свойству смежных углов <С= 180-60-50=70. Продлим прямые АС и СД. <ВСД=60=<В как накрест лежащие углы по свойству параллельных прямых при параллельных АС И СД и секущей ВС. <А= 180 -60 - 70= 50
12.ADB-равнобедренный,<А=<АВД=30.
<АДВ=180-30-30=120
<ДВС=<С,тк тр-к ДВС равнобедренный.
По теореме о внешнем угле <ДСВ=<С=120÷2=60
<В по теореме о сумме углов тр-ка равен 180-60-30=90