1) катет прямоугольного треугольника равен 30. Найдите расстояние от вершиныпрямого угла до гипотенузы, если радиус описснной около этого треугольника окружности равен 17. 2) гипотенуза равна 20. Найдите проекцию на гипотенузу катета, равного 8 корень 5. 3)проекция одного из катетов на гипотенузу равна 4. Найдите этот катет, если известно, что он меньше гипотенузы в корень 5 раз. В ответе указать число, равное квадрату искомого катета надо
ЕСли АВСД - прямоугольник,
1)значит пара сторон(векторов) параллельны АВ(3-4;5-1)=АВ(-1;4)
ДС(-1-0;4-0)=ДС(-1;4)
Чтобы найти координаты вектора из координат конца вектора вычел координаты начала АВ=ДС (это векторы) раз координаты векторов равны то и векторы равны значит параллельны
2)Диагонали прямоугольника равны) - это уже длины
Сначала найду координаты векторов: АС(-1-4;4-1)=АС(-5;3)
ВД(0-3;0-5) =ВД(-3;-5)
Теперь найду длину АС=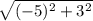 =
=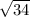 ВД=
ВД=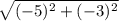 =
=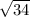
Так как АВ|| ДС; AB= СД; АС=ВД - это АВСД прямоугольник
Объяснение:
ответ:Высот у ромба 4 , но они равны между собой , если рассмотреть все треугольники , в которые входят эти высоты. Высоту ромба можно найти по тем формулам , исходя из того , какие данные изначально даны в задаче .
1 ) Допустим , дана площадь ромба S и его сторона а , тогда высота ромба h = S / a ,
2 ) Если даны диагонали ромба d1 и d2 , и сторона ромба а :,
h = (d1 * d2 ) / a ,
3 ) Если дана сторона а и угол между смежными сторонами А :
h = a * a * sin A / a = a * sin A.
Возможны другие варианты нахождения высоты ромба в зависимости от того , что будет дано в условии задачи. Но одними из основных данных параметров ромба являются а (сторона ромба ) , диагонали d1 , d2 , A (sin A). Посмотри может так чем смог