1. На боковых сторонах AB и СД трапеции Авсд (BC || АД) отмечены точки K и L соответственно, так, что угол BCK= угол ACK и угол CAL= угол ДАL. Оказалось, что прямые KL и АД параллельны. Найдите длину диагонали AC, если известно,
что BC=4 см, АД=9 см.

Показать ответ

Ответ:

варваритос2020

28.01.2020 13:19

32 cм²

Объяснение:

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:

Sбок= 1/2*(Р1+Р2)*L,

где Р1 и Р2 - периметры оснований пирамиды, L - апофема (высота боковой грани правильной усеченной пирамиды)

Найдём стороны оснований правильной четырехугольной усеченной пирамиды.

Диагональ квадрата: d = a√2, где а - сторона квадрата.

⇒ а = d/√2

АД = 6/√2 = 3√2, А1Д1= 2/√2 = √2.

Р1=4*АД= 4 * 3√2 = 12√2 см - периметр верхнего основания.

Р2=4*А1Д1=4√2 см - периметр нижнего основания пирамиды.

Найдем апофему L

Основания усеченной пирамиды - квадраты. Проведем из центров оснований перпендикуляры ОМ⊥ДС и О1М1⊥Д1С1. ОМ и О1М1 - радиусы вписанных окружностей в основания.

Т.к. r=a /2 (половина стороны основания), то

О1М1= А1Д1/2 =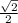 $\frac{\sqrt{2} }{2}$

ОМ = АД/2 =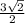 $\frac{3\sqrt{2} }{2}$

Опустим перпендикуляр М1К из точки М1 верхнего основания на нижнее основание. Получим прямоугольный ΔМ1КМ.

Т.к. М1К⊥КМ, КМ⊥ДС, то М1М⊥ДС ( по теореме о трёх перпендикулярах) ⇒∠М1МК = 60° (это данный нам линейный угол двугранного угла при ребре большего основания).

КМ = разнице расстояний от центров оснований до боковых сторон, то есть КМ = ОМ-О1М1=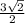 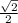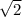$\frac{3\sqrt{2} }{2}$ - $\frac{\sqrt{2} }{2}$ = $\sqrt{2}$ см.

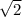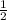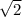Тогда гипотенуза (апофема) L = ММ1 = КМ / cos 60° = $\sqrt{2}$ : $\frac{1}{2}$ = 2 $\sqrt{2}$ cм

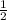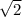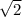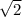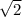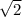Sбок = $\frac{1}{2}$ * ( 12 $\sqrt{2}$ + 4 $\sqrt{2}$ ) * 2 $\sqrt{2}$ = $\sqrt{2}$ (12+4) $\sqrt{2}$ = 2*16=32 cм²

диагонали основ правильной четырехугольной усеченной пирамиды равны 6 и 2 см, а двугранный угол при

0,0(0 оценок)

Ответ:

Hffjcdhudyhx

17.05.2020 03:58

Пифагор:Великий ученый Пифагор родился в 570 г. до н. э. на острове Самос. Отец Пифагора, Мнесарх, был ювелиром. Имя матери Пифагора неизвестно. По многочисленным записям родившийся ребенок был очень красив и, повзрослев, отличался уникальными .

Евклид:К наиболее достоверным сведениям о жизни Евклида принято относить то немногое, что приводится в комментариях Прокла к первой книге Начал Евклида (хотя следует принять во внимание, что Прокл жил спустя почти 800 лет после Евклида). Отметив, что «писавшие по истории математики» не довели изложение развития этой науки до времени Евклида, Прокл указывает, что Евклид был моложе Платоновского кружка, но старше Архимеда и Эратосфена, «жил во времена Птолемея I Сотера», «потому что и Архимед, живший при Птолемее Первом, упоминает об Евклиде и, в частности, рассказывает, что Птолемей спросил его, есть ли более короткий путь изучения геометрии, нежели Начала; а тот ответил, что нет царского пути к геометрии»

Арихимед:Впервые биография Архимеда была описана неким Гераклидом, вероятно, его учеником. Она существовала ещё в VI веке н. э., так как её упоминает математик Евтокий Аскалонский в комментариях к работам античного учёного[2]. Наиболее ранние из дошедших до современников сведения об Архимеде содержатся в «Истории» Полибия (200—120 годы до н. э.). Этот историк подробно рассказывает о созданных сиракузским учёным машинах[3].

Объяснение:

это все что я знаю

0,0(0 оценок)

Популярные вопросы: Геометрия