1. Накресліть прямокутник ABCD. Побудуйте: а) відрізок, симетричний діагоналі BD відносно прямої АС;
б) кут, симетричний куту ADB відносно точки В.

2. Дано точки А(-1; – 3), В(1;1), C(3; – 3). Знайдіть координа-
ти точки, симетричної початку координат відносно:
а) осі симетрії трикутника ABC;
б) основи медіани AM трикутника ABC.

Показать ответ

Ответ:

elizavetaivlic

07.08.2021 00:23

ответ:

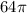$64\pi$ см³.

Объяснение:

Обозначим данную пирамиду буквами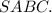 SABC.

AB = 12 см.

Проведём высоту пирамиды SO.

$\angle SAO = 30^{\circ}$

Начертим около этой пирамиды конус.

Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.

=======================================================

Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.

$\Rightarrow AB = BC = AC = 12$ см.

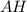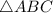
Проведём высоту в $\triangle ABC$

$\triangle SAO$ - прямоугольный, так как - высота пирамиды.

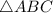$\triangle ABH$ - прямоугольный, так как - высота $\triangle ABC$ .

Так как $\triangle ABC$ - равносторонний ⇒ 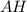- высота, медиана и биссектриса

BH = HC = BC:2 = 12:2 = 6 см, так как - медиана.

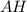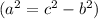Найдём по теореме Пифагора (a^2 = c^2 - b^2) .

$AH = \sqrt{AB^2 - BH^2} = \sqrt{12^2 - 6^2} = \sqrt{108} = 6\sqrt{3}$ см.

Точка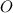 - пересечение медиан и делит их в отношении 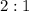2:1 , считая от вершины.

$\Rightarrow AO = 2/3\cdot AH = 2/3 \cdot 6\sqrt{3} = 4\sqrt{3}$ см

$OH = 1/3\cdot AH = 1/3 \cdot 6\sqrt{3} = 2\sqrt{3}$ см.

Также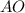 - радиус описанной около 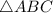$\triangle ABC$ окружности.

Рассмотрим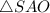 $\triangle SAO$

Если угол в прямоугольном треугольнике равен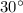 $30^{\circ}$ , то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow SA = 2SO$

Составим уравнение:

Пусть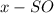 x - SO , тогда 2x - SA .

И по теореме Пифагора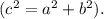 (c^2 = a^2 + b^2).

$(4\sqrt{3})^2 + x^2 = (2x)^2\\\\48 + x^2 = 4x^2\\\\-3x^2 =-48\\\\x^2 =16 \\\\x= 4$

конуса = $1/3 \cdot \pi \cdot AO^2 \cdot SO = \pi \Big(1/3 \cdot (4\sqrt{3})^2 \cdot 4\Big) = 64\pi$ см³.

Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к пл

0,0(0 оценок)

Ответ:

aaapruda

18.11.2020 20:43

1. а)Уравнение окружности х²+у²=1 этой окружности принадлежит точка В(√3/2;-1/2), т.к. подставляя в уравнение окружности, получим

3/4+1/4=1. остальные не подходят.

б) Эта точка лежит в четвертой четверти, ей соответствует угол 330°, или в радианной мере 11π/6; косинус этого угла равен абсциссе точки, т.е. √3/2, синус - ее ординате, т.е. -1/2, тангенс - отношение синуса к косинусу, т.е. -1/√3=-√3/3, а котангенс обратен тангенсу, и равен -√3. Проверим, например синус sin330°=sin(360°-30°)=sin30°=-1/2

cos330°=cos(360°-30°)=cos(-30°)=cos30°=√3/2

2. по теореме косинусов х²=а²+b²-2ab*cosα; третья сторона х=√(25+16-2*4*5*0.5)=√21/см/; периметр равен 4+5+√21=(9+√21)/см/

Площадь найдем по формуле s=(a*b*sinα)/2=(4*5*sin60°)/2=20√3/см²/

Радиус окружности, описанной около этого треугольника найдем по следствию из теоремы синусов. а/sinα=2R⇒R=a/(2sinα)=

√21/(2√3/2)=√7/cм/

3. по теореме синусов 12/sin50°=32/sinα⇒sinα=32*sin50°/12=

32*0.766/12≈2/043, решений ноль, т.к. не может синус угла быть больше единицы.