1. Найдите координаты точек, симметричных точкам M (−6; 8) и K (0; −2) относительно: 1) оси абсцисс; 2) оси ординат; 3) начала координат.
2. Начертите треугольник ABC. Постройте образ треугольника ABC: 1) при параллельном переносе на вектор ; 2) при симметрии относительно точки B; 3) при симметрии относительно прямой AC.
3. Точка A1 (х ; −4) является образом точки A (2; y) при гомотетии с центром H (1; −2) и коэффициентом k = −3. Найдите x и y.
4. Прямая, параллельная стороне AC треугольника ABC, пересекает его сторону AB в точке M, а сторону BC — в точке K. Найдите площадь трапеции AMKC, если BM = 4 см, AM = 8 см, а площадь треугольника MBK равна 5 см2.
5. Из точек A и B, лежащих в одной полуплоскости относительно прямой a, опущены перпендикуляры AA1 и BB1 на эту прямую. Известно, что
AA1 = 4 см, BB1 = 2 см, A1B1 = 3 см. Какое наименьшее значение может принимать сумма AX + XB, где X — точка, принадлежащая прямой a?
В ромбе диагонали точкой пересечения делятся пополам (АО=ОС и ВО=OD).
Пусть ВО=х, тогда:
AC-BD=14
AC-2x=14
AC=14+2x
2·OC=2(x+7)
OC=x+7
Из ΔBCO по т. Пифагора:
x=-15 не подходит по смыслу задачи, поэтому один корень х=8.
ВО=х=8 см
ОС=х+7=8+7=15 см
АС=АО+ОС=15+15=30 см
BD=BO+OD=8+8=16 см
Вспомним такую формулу: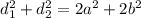 , где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
, где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
Найдем диагонали, составив систему:
Пусть АС=х, BD=y.
Отрицательные значения нам не подходят, так как длинна - величина неотрицательная.
Тогда AC=x=30см, BD=y=16см.
ответ: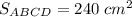
Объяснение:
d₁-d₂=14
d₁=14+d₂
Діагоналі у точці перетину діляться навпіл і утворюють прямокутні трикутники.Катети дорівнюють половинам діагоналей: 14+d₂ / 2 та d₂/2.
За теоремою Піфагора:
17²=(14+d₂ /2)²+ (d₂/2)²
289=(14+d₂)² /4+d₂²/4
289*4=(14+d₂)² +d₂²
1156=14²+28d₂+d₂²+d₂²
2d₂²+28d₂-960=0 :2
d₂²+14d₂-480=0
D = b² - 4ac = 14² - 4·1·(-480) = 196 + 1920 = 2116
x₁ = -14 - √2116 /2·1 = -14 - 46/ 2 = -60 /2 = -30 не підходить
x₂ = -14 + √2116/ 2·1 = -14 + 46 /2 = 32/ 2 = 16 см -d₂
d₁=16+14 = 30 см
S=1/2× 16×30=240 см²