Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
Объяснение:
Основы равнобедренной трапеции равны 10 см и 18 см. Найдите отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание.
Дано: ABCD - равнобедренная трапеция.
ВС = 10 см; AD = 18 см.
ВЕ - высота.
Найти: BC и AD.
Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований, а большая - полусумме оснований.
⇒ АЕ = (AD - BC) : 2 = (18 - 10) : 2 = 4 (см)
ED = (AD + BC) : 2 = (18 + 10) : 2 = 14 (см)
Докажем это свойство.
Пусть ВС = а, а AD = b.
Опустим еще один перпендикуляр CH на AD.
Рассмотрим ЕВСН.
ВС || EH (условие)
ВЕ ⊥ AD; CH ⊥ AD.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ BE || CH.
ЕВСН - параллелограмм (по определению)
Все углы прямые.
⇒ ЕВСН - прямоугольник.
В прямоугольнике противоположные стороны равны.
⇒ ВС = ЕН = а
Рассмотрим ΔАВЕ и ΔHCD - прямоугольные.
АВ = CD (ABCD - равнобедренная трапеция)
Углы при основании равнобедренной трапеции равны.
∠A = ∠D
ΔАВЕ = ΔHCD (по гипотенузе и острому углу)
⇒
ED = HD + EH
Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
ответ: Координаты точки B (10;1).
Объяснение:
Точка А (2; 5) один из концов отрезка AB. Точка C (6; 3) - середина отрезка АВ Найди координаты точки В.
Дано: ,
, 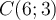 - середина отрезка АВ
- середина отрезка АВ
Найти:
Координата середины отрезка равна полусумме соответствующих координат его концов:
x = (x₁+x₂)/2 и y = (y₁+y₂)/2 ⇒ найдём другой конец отрезка АВ:
Координаты точки B (10;1)
#SPJ1
Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
Объяснение:
Основы равнобедренной трапеции равны 10 см и 18 см. Найдите отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание.
Дано: ABCD - равнобедренная трапеция.
ВС = 10 см; AD = 18 см.
ВЕ - высота.
Найти: BC и AD.
Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований, а большая - полусумме оснований.⇒ АЕ = (AD - BC) : 2 = (18 - 10) : 2 = 4 (см)
ED = (AD + BC) : 2 = (18 + 10) : 2 = 14 (см)
Докажем это свойство.
Пусть ВС = а, а AD = b.
Опустим еще один перпендикуляр CH на AD.
Рассмотрим ЕВСН.
ВС || EH (условие)
ВЕ ⊥ AD; CH ⊥ AD.
Если две прямые перпендикулярны третьей, то они параллельны между собой.⇒ BE || CH.
ЕВСН - параллелограмм (по определению)
Все углы прямые.
⇒ ЕВСН - прямоугольник.
В прямоугольнике противоположные стороны равны.⇒ ВС = ЕН = а
Рассмотрим ΔАВЕ и ΔHCD - прямоугольные.
АВ = CD (ABCD - равнобедренная трапеция)
Углы при основании равнобедренной трапеции равны.∠A = ∠D
ΔАВЕ = ΔHCD (по гипотенузе и острому углу)
⇒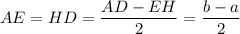
ED = HD + EH
Отрезки, на которые высота, проведенная с вершины тупого угла, делит большое основание равны 4 см и 14 см.
#SPJ1