1. Найдите полную поверхность конуса с образующей l=6 и кругом радиуса R=3 в основании.
2. Найдите объем пирамиды с высотой Н, равной 22 см, в основании которой лежит равносторонний треугольник со стороной a=5.
3.Найдите объем конуса с высотой Н, равной 4 см, и кругом в основании радиуса R=15.
1) 84.78
2) 79.38
3) 942.47
Объяснение:
1) Формула поверхности конуса находится по формуле:
S = s1 + s2, где
s1 - площадь основания, находится по формуле: s1 = pi*r²
s2 - площадь поверхности, находится по формуле: s2 = pi*r*l
s1 = 3.14*3^2 = 28.26
s2 = 3.14*3*6 = 56.62
S = 28.26 + 56.62 = 84.78
2) Объем пирамиды: V = 1/3 * S * H, где:
S - площадь основания (в данном случае треугольника)
H - высота пирамиды
найдем площадь треугольника в основании:
площадь равностороннего треугольника находится по формуле:
S = a² *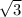 /4, a - длина стороны треугольника
/4, a - длина стороны треугольника
S = 5^2 *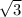 /4 = 6.25 *
/4 = 6.25 * 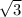
V = 1/3 * 6.25 *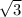 *22 = 79.38
*22 = 79.38
3) Объем конуса также как и объем пирамиды: V = 1/3 * S * H
В данном случае на основании лежит круг, нужно найти его площадь
S = pi*r^2=3.14*15*15 = 706.8
V = 1/3 * S * H = 1/3 * 706.8 * 4 = 942.47