1. Осевым сечение конуса является равносторонний треугольник со стороной 40 см. Найди объем конуса.
2. Найти объем тела вращения, образованной при вращении прямоугольной трапеции вокруг стороны, перпендикулярной основанию трапеции, если площадь трапеции равна 68 см2, основания равны 7 см и 10 см.
3. Найдите площадь поверхности и объем шара, если радиус шара равно 3,5 дм.
Для построения серединного перпендикуляра надо:
построить две окружности - с центром в точке А и с центром в точке С, произвольного радиуса, но больше половины длины отрезка АС;
у этих окружностей найти точки пересечения - К и М;
Через точки пересечения окружностей провести прямую а.
Эта прямая - серединный перпендикуляр.
Затем этот серединный перпендикуляр надо продлить до пересечения со стороной ВС. Точка пересечения серединного перпендикуляра и стороны ВС - искомая точка (на чертеже это точка О).
Обратите внимание, в зависимости от треугольника задача может и не иметь решение. На первом чертеже точка О лежит на стороне ВС - задача имеет решение, на втором чертеже точка О не лежит на стороне ВС, а находится на продолжении этой стороны, на третьем такую точку совсем не построить.
В этой задаче необходимо провести исследование и выяснить, когда задача имеет решение.
1) Пусть сторона основания равнобедренного треугольника равна х см, тогда боковые стороны равны (x+10) см. Зная, что периметр равнобедренного треугольника равен 98 см, составим уравнение
x + 2(x+10) = 98
x + 2x + 20 = 98
3x = 78
x = 26 см - сторона основания
Боковые стороны равнобедренного треугольника 26 + 10 = 36 см.
2) Теперь примем за х боковую сторону равнобедренного треугольника, тогда сторона основания равна (x+10) см. Составим уравнение
x + 10 + 2x = 98
3x = 88
x = 88/3 см - боковая сторона
88/3 + 10 = 118/3 см - сторона основания
Т.е. у обеих вариантов выполняется неравенство треугольника, значит данная задача имеет два решения.
ответ: 26 см, 36 см, 36 см или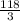 см,
см, 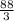 см,
см, 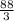 см.
см.