1. Основою прямого паралелепіпеда є: *
а) прямокутник;
б) паралелограм;
в) квадрат;
г) ромб.
2. Вершина піраміди проектується в центр вписаного кола. В даній піраміді рівні: *

а) бічні ребра;
б) висоти бічних граней;
в) і бічні ребра, і висоти бічних граней;
г) визначити не можливо.
3. Основа призми – квадрат. Дана призма є: *

а) прямою;
б) правильною;
в) похилою;
г) визначити неможливо.
4.Бічна поверхня куба 64 см^2. Знайти об’єм куба. *

а) 64
б) 96
в) 128
г) 192
5.Сторона основи правильної трикутної призми дорівнює 6 см, а висота призми – 5 см. Обчисліть площу бічної поверхні призми. *

а) 30
б) 180
в) 60
г)90
6.Основа паралелепіпеда - прямокутник, бічні ребра нахилені до площини основи під кутом 75^0. Даний паралелепіпед є: *

а) прямокутним;
б) прямим;
в) визначити неможливо;
г) похилим
7.Сторона основи правильної чотирикутної піраміди дорівнює 2 см, а висота піраміди - 2√2 см. Знайдіть площу повної поверхні піраміди.

8.Основою паралелепіпеда є ромб з стороною 8 см і гострим кутом 60°. Більша діагональ паралелепіпеда утворює з площиною основи кут 30°. Знайти об’єм паралелепіпеда.

Показать ответ

Ответ:

Nbveh1234567890

30.10.2021 18:40

В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды

Объяснение:

Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.

Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.

S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .

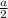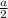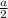
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁= $\frac{a}{2}$ Пусть Р₁К⊥ОР, тогда КР=а- $\frac{a}{2}$ = $\frac{a}{2}$

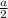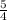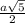Из ΔКРР₁ по т. Пифагора Р₁К=√(а²+( $\frac{a}{2}$ )²)=а√ $\frac{5}{4}$ = $\frac{a\sqrt{5} }{2}$ .

S( бок. усеч. пир.)=4*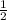 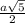$\frac{1}{2}$ * $\frac{a\sqrt{5} }{2}$ *(a+2a)=3a²√5 (ед²).

надо через несколько дней.задача: в правильной четырехугольную усеченую пирамиду вписан куб так, сто

0,0(0 оценок)

Ответ:

happymenfeed

06.04.2022 05:48

Объяснение:

Скалярное произведение векторов

Скалярным произведением векторов a(x1;y1;z1) и b(x2;y2;z2), заданных своими координатам, находится по формуле:

Скалярное произведение векторов

Зная модули векторов и угол между ними, скалярное произведение можно найти по формуле:

Условие перпендикулярности векторов a(x1;y1;z1) и b(x2;y2;z2) имеет вид:

x1x2 + y1y2 + z1z2 = 0

Решение онлайн

Видеоинструкция

ИНСТРУКЦИЯ. Заполните координаты векторов и нажмите кнопку Решение. При этом векторы могут быть заданы на плоскости (две координаты) и в пространстве (три координаты).

Задание. Найти скалярное произведение векторов

Заданы

две координаты вектора

три координаты вектора

a = (

;

) и b = (

;

)

Решение

ПРИМЕР. Найти скалярное произведение векторов a = (4; -3; 1) и b = (5; -2; -3).

Решение. По формуле находим a·b = 4·5 + (-3)·(-2) + 1·(-3) = 23. Поскольку 23≠0, то данные вектора не перпендикулярны.