1. Площадь основания цилиндра - 36 п. См2, высота - 8 см. Найдите объем цилиндра. A) 180p см3 B) 144p см3 C) 288p см3 D) 360p см3 E) 200p см3 2. Площадь осевого сечения цилиндра составляет 24 см2. Найдите площадь боковой поверхности цилиндра. A) 24p см2 B) 36 см2 C) 68 см2 D) 8p см2 E) 72 см2 3. Площадь основания цилиндра 25 п см2, длина создателя 24 см. Найдите диагональ осевого сечения цилиндра. A) 23 см B) 24 см C) 25 см D) 26 см E) 27 см 4. Радиус основания цилиндра 2 м, высота 3 м. Найдите размер. A) 25pm3 B) 12pm3 C) 10pm3 D) 5pm3 E) 15pm3 5. Основание цилиндра имеет радиус 2 м и высоту 3 м. Найдите диагональ осевого сечения. A) 1 м B) 25 м C) 5 м D) 10 м E) м
У квадрата все стороны равны и его периметр составляет сумму длин всех четырех сторон или учетверенный размер одной стороны:
Р = а + а + а + а = 4 * а,
Где а - сторона квадрата.
То увеличение стороны квадрата на 25%, при условии, что фигура остается квадратом, влечет за собой увеличение всех сторон квадрата на 25% и значит, увеличивает периметр на длину одной стороны. Продемонстрируем.
Старая сторона квадрата составляла 100%, а новая составляет:
100% + 25% = 125%;
И равна:
b = а * 125 / 100 = 1,25 * а.
Новый периметр составит:
Рн = b + b + b + b = 4 * b = 4 * 1,25 а = 5 * а.
Найдем разницу периметров:
Рн - Р = 5 * а - 4 * а = а.
То есть разница между периметрами при увеличении стороны квадрата на 25% составляет длину одной стороны изначального квадрата.
1) ∡МНО = 45
2)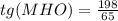
Объяснение:
Рассчитайте величину двугранного угла при основании правильной четырехугольной пирамиды если:
1.сторона основания равна 3,6 м, а высота равна 1,8 м
(ABCD-квадрат) а = 3,6
ΔMOH OH = 0.5a=1.8; OM ⊥ OH; MO= 1,8 ⇒ ΔMOH прямоугольный равнобедренный ОМ = ОН = 1,8; ∡МОН = 90° ⇒ ∡МНО = 45
2.сторона основания равна 65 см, а высота равна 99 см
(ABCD-квадрат) а = 65
ΔMOH OH = 0.5a=65/2 OM ⊥ OH; MO= 99 ⇒ ΔMOH прямоугольный ∡МОН = 90° ⇒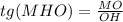
известен тангенс угла, а следовательно и сам угол при необходимости можно найти по таблицам Брадиса