1) Прямая a пересекает плоскость β в точке C и образует с плоскостью угол 30°, В ∈a, точка А - проекция точки В на плоскость β, ВC=12 см. Найдите ВА.
2) К плоскости α проведена наклонная AС (A∈α). Длина наклонной равна 24 см, наклонная
с плоскостью образует угол 60°. Вычислите, на каком расстоянии от плоскости находится
точка С.
3) Наклонная AК с плоскостью α образует угол 30°, а наклонная КC с плоскостью α
образует угол 45°. Длина перпендикуляра КB равна 12 см. Вычислите длины наклонных

Показать ответ

Ответ:

SanchesMaster

24.01.2023 07:22

В равностороннем треугольнике АВС со стороной, равной √3, проведены три биссектрисы : AM, BH, CK. Найдите периметр треугольника ALH.

- - -

Дано :

ΔАВС - правильный (равносторонний).

АВ = √3.

АМ, ВН, СК - биссектрисы.

АМ ∩ ВН ∩ СК = L.

Найти :

Р(ΔALH) = ?

АВ = ВС = АС = √3 (по определению равностороннего треугольника).

В правильном треугольнике все его биссектрисы являются медианами и высотами.

Соответственно, по определению медианы треугольника -

АН = НС =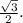 $\frac{\sqrt{3} }{2}.$

Рассмотрим ΔALH - прямоугольный (так как ∠AHL= 90° по определению высоты).

В равностороннем треугольнике все углы равны по 60°.

То есть ∠А = 60°.

По определению биссектрисы треугольника -

∠ВАМ = ∠МАС = 60°/2 = 30°.

По определению косинуса острого угла прямоугольного треугольника -

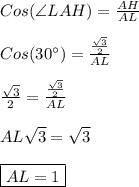
$Cos(\angle LAH) = \frac{AH}{AL}\\\\Cos(30^{\circ} ) = \frac{\frac{\sqrt{3} }{2} }{AL} \\\\\ \frac{\sqrt{3} }{2} = \frac{\frac{\sqrt{3} }{2} }{AL}\\\\AL\sqrt{3} = \sqrt{3} \\\\\boxed{AL = 1}$

В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузе.

Отсюда -

LH = 0,5*AL = 1*0,5 = 0,5.

Периметр - это сумма длин всех сторон.

Отсюда -

Р(ΔALH) = LH + AL + AH =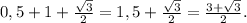 $0,5 + 1 + \frac{\sqrt{3} }{2} = 1,5 + \frac{\sqrt{3} }{2} = \frac{3+\sqrt{3} }{2}.$

$\frac{3+\sqrt{3} }{2}$ (ед).

0,0(0 оценок)

Ответ:

Ferolhr129

24.08.2022 12:44

Обозначим прямоугольник, как АВСД

Значит, мы уже знаем, что периметр прямоугольника равен 20 см, а одна его сторона 8

Следовательно, по свойству прямоугольника ВС = АД = 8, значит АВ=СД= 20 - 8 +8) = 4

АВ=СД=2 см

Теперь ищем площадь прямоугольника АВСД

Площадь АВСД = ВС * АВ = 8 * 2 = 16

Мы знаем, по условию, что площади прямоугольника и квадрата равны

Площадь квадрата находится очень просто, надо одну его сторону возвести в квадрат.

Обозначим квадрат, как НПРО, следовательно

площадь квадрата будет = НП в квадрате. Площадь нам уже известна, она равна 16, а единственное число, которое при возведение в квадрат даёт 16, это число 4

Значит, сторона НП = 4

У квадрата все стороны равны, следовательно, что бы найти периметр квадрата, нам нужно просто сложить все четыре стороны.

Периметр квадрата = 4 + 4+ 4+ 4 = 16

Периметр квадрата равен 16

ответ: 16

0,0(0 оценок)

Популярные вопросы: Геометрия