1) Расстояние от центра шара до секущей плоскости 0,6 м. Вычислите площадь сферы, если радиус сечения 0,8 м. 2) Основанием прямой призмы является параллелограмм АВСD, АВ = 4 см, ВС = 6 см, угол АВС = 450. Найдите объем призмы, если ее боковое ребро 8 см решить
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L =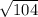
= 2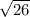
≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So =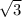
a²/4=4
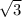. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6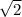
, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3
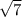, площадь основания So=a²=36, объём V=Soh/3=36
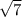≈ 95,25 ≈ 95 см²
cos (A + B) = cos (180 – C) = –cos C.
Данное равенство переписывается так:
cos A + cos B + cos C = ³⁄₂. (1)
Докажем, что из (1) следует A = B = C = 60°.
Для произвольного треугольника
cos A + cos B = 2 cos ½(A + B) cos ½(A – B), (2)
cos ½(A + B) = cos ½(180° – C) = cos (90° – ½C) = sin ½C. (3)
Равенство (3) показывает, что cos ½(A + B) — положительная величина, поэтому из (2) следует, что
cos A + cos B ≤ 2 cos ½(A + B) = 2 sin ½C.
Следовательно,
cos A + cos B + cos C ≤ 2 sin ½C + cos C = 2 sin ½C + 1 – 2 sin² ½C =
= –2(sin ½C – ½)² + ³⁄₂.
Значит, для любого треугольника
cos A + cos B + cos C ≤ ³⁄₂,
причём равенство достигается при sin ½C = ½, cos ½(A – B) = 1, т. е. при A = B = C = 60°.
Итак, треугольник ABC правильный. Сторона равна 18/3 = 6. Биссектрисы (они же высоты и медианы) все три равны 3√3. Площадь (правильного) треугольника из них равна
¼√3 (3√3)² = ²⁷⁄₄√3.