Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Тк объемы равны то если r1 и r2 радиусы оснований а h1 и h2 вычосы цилиндров то их объемы равны pi*r1^2*h1 и pi*r2^2*h2 тогда тк объемы равны то сократив на pi r1^2*h1=r2^2*h2 найдем теперь их боковые поверхности s1=2*pi*r1*h1 s2=2*pi*r2*h2 деля их друг на друга получим сократив на 2pi s1/s2=r1*h1/r2*h2 из 1 равенства следует что r1^2*h1/r2^2*h2=1 тогда преобразовав наше выражение следующим образом имеем s1/s2=(r1^2*h1/r2^2*h2*)*(r2/r1)=r2/r1 то есть s1/s2=r2/r1 то есть боковые поверхности обратно пропорциональны радиусам что и требовалось доказать
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их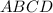
и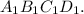 
Проведём диагональ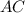
в квадрате 
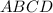и диагональ 
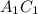в квадрате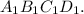 
Рассмотрим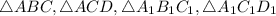
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.