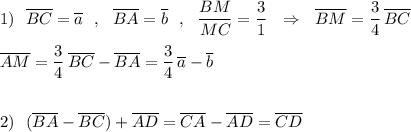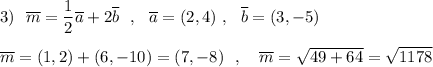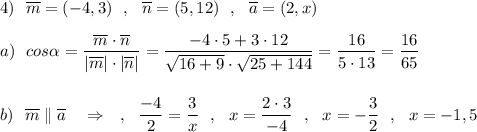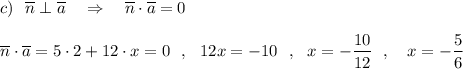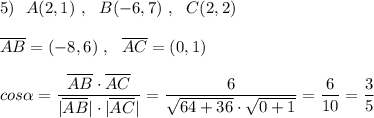1. Точка М лежит на стороне ВС параллелограмма АВСД, причем ВМ : МС = 3 : 1. Выразите вектор (АМ ) ⃗ через векторы (ВС) ⃗ = a ⃗ и (ВА) ⃗ = b ⃗ .
2. АВСД – параллелограмм. Найдите (ВА) ⃗ – (ВС) ⃗ + (АД) ⃗.
3. Найдите модуль вектора m ⃗ = – 1/2 a ⃗ + 2b ⃗, где a ⃗ = 2i ⃗ + 4j ⃗ и b ⃗ = 3i ⃗ – 5j ⃗
4. Даны векторы m ⃗(–4; 3), n ⃗(5; 12), a ⃗(2; х). Найдите:
а) косинус угла между векторами m ⃗ и n ⃗ ;
б) число х, если векторы ( m) ⃗ и ( a) ⃗ коллинеарны;
в) число х, если векторы n ⃗ и ( a) ⃗ перпендикулярны.
5. Даны вершины треугольника АВС: А(2; 1), В(−6; 7) и С(2; 2).
Найдите косинус угла А.

Показать ответ

Ответ:

Вика310387

28.11.2020 06:24

$1)\ \ \overline{BC}=\overline{a}\ \ ,\ \ \overline{BA}=\overline{b}\ \ ,\ \ \dfrac{BM}{MC}=\dfrac{3}{1}\ \ \Rightarrow \ \ \overline{BM}=\dfrac{3}{4}\, \overline{BC}\\\\\overline{AM}=\dfrac{3}{4}\, \overline{BC}-\overline{BA}=\dfrac{3}{4}\, \overline{a}-\overline{b}\\\\\\2)\ \ (\overline{BA}-\overline{BC})+\overline{AD}=\overline{CA}-\overline{AD}=\overline{CD}$

$3)\ \ \overline{m}=\dfrac{1}{2}\overline{a}+2\overline{b}\ \ ,\ \ \overline{a}=(2,4)\ ,\ \ \overline{b}=(3,-5)\\\\\overline{m}=(1,2)+(6,-10)=(7,-8)\ \ ,\ \ \ \overline{m}=\sqrt{49+64}=\sqrt{1178}$

$4)\ \ \overline{m}=(-4,3)\ \ ,\ \ \overline{n}=(5,12)\ \ ,\ \ \overline{a}=(2,x)\\\\a)\ \ cos\alpha =\dfrac{\overline{m}\cdot \overline{n}}{|\overline{m}|\cdot |\overline{n}|}=\dfrac{-4\cdot 5+3\cdot 12}{\sqrt{16+9}\cdot \sqrt{25+144}}=\dfrac{16}{5\cdot 13}=\dfrac{16}{65}\\\\\\b)\ \ \overline{m}\parallel \overline{a}\ \ \ \Rightarrow \ \ \ ,\ \ \dfrac{-4}{2}=\dfrac{3}{x}\ \ ,\ \ x=\dfrac{2\cdot 3}{-4}\ \ ,\ \ x=-\dfrac{3}{2}\ \ ,\ \ x=-1,5$

$c)\ \ \overline{n}\perp \overline{a}\ \ \ \Rightarrow \ \ \ \overline{n}\cdot \overline{a}=0\\\\\overline{n}\cdot \overline{a}=5\cdot 2+12\cdot x=0\ \ ,\ \ 12x=-10\ \ ,\ \ x=-\dfrac{10}{12}\ \ ,\ \ \ x=-\dfrac{5}{6}$

$5)\ \ A(2,1)\ ,\ \ B(-6,7)\ ,\ \ C(2,2)\\\\\overline{AB}=(-8,6)\ ,\ \ \overline{AC}=(0,1)\\\\cos\alpha =\dfrac{\overline{AB}\cdot \overline{AC}}{|\overline{AB}|\cdot |\overline{AC}|}=\dfrac{6}{\sqrt{64+36}\cdot \sqrt{0+1}}=\dfrac{6}{10}=\dfrac{3}{5}$