1. У призмі площа бічної поверхні дорівнює 109см², а площа повної поверхні -165см². Знайдіть площу основи 2. Площа бічної поверхні правильної семикутної піраміди дорівнює 350см². Знайдіть площу однієї бічної грані цієї піраміди
3. Висота похилої призми дорівнює 36см. Знайдіть бічне ребро призми, якщо воно утворює з площиною основи кут 45°.
4. Сторони основи прямокутного паралелепіпеда дорівнюють 5см і 12см, а висота 8 см. Знайдіть площу діагонального перерізу паралелепіпеда
5. Апофема правильної чотирикутної піраміди дорівнює 16см, а сторона основи 10см. Знайдіть площу повної поверхні піраміди
6. У правильній трикутній призмі медіана основи дорівнює 6√3. Знайдіть площу бічної поверхні цієї призми, якщо діагональ бічної грані утворює з висотою кут 45°.
1)
1. E
2. F
3. B
4. E
5. A
6. D.
Теорема косинусов: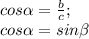
Теорема синусов: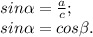
3)
Формула вычисления стороны, зная 2 другие, и угол между ними:
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова: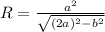
Формула вычисления вписанной окружности около равнобёдренного треугольника такова: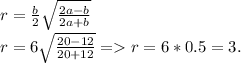
Углы параллелограмма: 60°, 60°, 120°, 120°
Объяснение:
CD = AB = 5√2 cм как противолежащие стороны параллелограмма.
ΔACD: по теореме синусов:
CD/sin 45° = AC/sin∠ADC
5√2 / (√2/2) = 5√3/sin∠ADC
sin∠ADC = 5√3/10 = √3/2
1. ∠ADC - острый
∠ADC = 60°, тогда ∠АСВ = 180° - ∠ADC = 120° (сумма углов параллелограмма, прилежащих к одной стороне, равна 180°)
2. ∠ADC - тупой.
∠ADC = 120°, тогда ∠АСВ = 180° - ∠ADC = 60°
В параллелограмме противолежащие углы равны.
ответ: Углы параллелограмма: 60°, 60°, 120°, 120°.