1) В параллелограмме ABCD точка M – середина BC, а точка K – середина AD. Найдите отношение длин отрезков, на которые прямые AM и CK разделили диагональ BD.
В параллелограмме ABCD точка M – середина BC, а точка K – середина AD. Найдите отношение длин отрезков, на которые прямые AM и CK разделили диагональ BD.
Объяснение:
1) Т.к. ABCD-параллелограмм, то ВС=АD ⇒ MC=AK.
Тогда АМСК- параллелограмма по признаку о двух равных и параллельных сторонах (MC=AK, MC ║AK) ⇒ АМ║КС.
В параллелограмме ABCD точка M – середина BC, а точка K – середина AD. Найдите отношение длин отрезков, на которые прямые AM и CK разделили диагональ BD.
Объяснение:
1) Т.к. ABCD-параллелограмм, то ВС=АD ⇒ MC=AK.
Тогда АМСК- параллелограмма по признаку о двух равных и параллельных сторонах (MC=AK, MC ║AK) ⇒ АМ║КС.
2)По т. Фалеса для ∠СВD получаем ВР=РН.
По т. Фалеса для ∠ADB получаем РН=НD.
Тогда ВР=РН=НD.
Поэтому отношение длин отрезков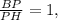
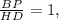
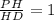 .
.